Persamaan Diophantine adalah sebuah persamaan suku banyak di mana variabel – variabel yang terlibat didefinisikan atas bilangan bulat. Nama Diophantine sendiri diambil dari seorang matematikawan bernama Diophantus, yang mempelajari tipe persamaan tersebut pada abad ke-3. Ia juga merupakan salah satu matematikawan yang mengenalkan simbol pada bidang aljabar. Bidang yang mempelajari masalah-masalah pada persamaan Diophantine saat ini dikenal dengan nama Diophantine analysis atau analisis Diophantine. Masalah yang dipelajari biasanya terkait dengan mencari eksistensi solusi, banyak solusi, atau cara untuk mendapatkan semua solusi.
Secara umum, persamaan Diophantine terbagi menjadi dua kategori, yakni persamaan Diophantine linear dan persamaan Diophantine non-linear. Persamaan Diophantine linear hanya melibatkan suku banyak berorder ![]() , sedangkan persamaan Diophantine non-linear melibatkan suku banyak berorder lebih dari
, sedangkan persamaan Diophantine non-linear melibatkan suku banyak berorder lebih dari ![]() . Di samping itu, terdapat juga tipe persamaan Diophantine di mana suku pada pangkat yang terlibat berupa suatu variabel. Persamaan ini dikenal dengan persamaan Diophantine eksponensial.
. Di samping itu, terdapat juga tipe persamaan Diophantine di mana suku pada pangkat yang terlibat berupa suatu variabel. Persamaan ini dikenal dengan persamaan Diophantine eksponensial.
Pada artikel ini akan dibahas mengenai persamaan Diophantine linear.
Secara umum, persamaan Diophantine linear dapat dinyatakan ke dalam bentuk
(1) ![]()
dengan ![]() merupakan bilangan bulat dan
merupakan bilangan bulat dan ![]() untuk setiap
untuk setiap ![]() .
.
Tipe masalah yang umumnya ditanyakan pada pesamaan Diophantine linear adalah mencari solusi bulat persamaan tersebut. Tentunya dalam mencari solusi, perlu diselidiki terlebih dahulu apakah persamaan tersebut memiliki solusi bulat atau tidak. Teorema di bawah ini memberikan syarat cukup dan perlu kapan suatu persamaan Diophantine linear memiliki solusi bulat.
Teorema 1. [Identitas Bezout]
[box] Persamaan (1) memiliki solusi bulat jika dan hanya jika ![]() habis membagi
habis membagi ![]() . Lebih lanjut, jika persamaan (1) memiliki solusi bulat, maka semua solusi bulat dari persamaan (1) dapat dinyatakan ke dalam
. Lebih lanjut, jika persamaan (1) memiliki solusi bulat, maka semua solusi bulat dari persamaan (1) dapat dinyatakan ke dalam ![]() parameter. [/box]
parameter. [/box]
[learn_more caption=”Bukti:” state=”open”]
Untuk mempermudah penulisan, misalkan ![]() .\\
.\\
\noindent ![]() Misalkan persamaan (1) memiliki solusi bulat. Andaikan
Misalkan persamaan (1) memiliki solusi bulat. Andaikan ![]() tidak habis dibagi oleh
tidak habis dibagi oleh ![]() . Perhatikan bahwa ruas kiri dari persamaan (1) habis dibagi oleh
. Perhatikan bahwa ruas kiri dari persamaan (1) habis dibagi oleh ![]() , sedangkan ruas kanannya tidak. Terjadi suatu kontradiksi. Dengan demikian,
, sedangkan ruas kanannya tidak. Terjadi suatu kontradiksi. Dengan demikian, ![]() habis dibagi oleh
habis dibagi oleh ![]()
\noindent ![]() Misalkan
Misalkan ![]() habis membagi
habis membagi ![]() . Diperoleh bahwa persamaan (1) ekuivalen dengan
. Diperoleh bahwa persamaan (1) ekuivalen dengan
(2) ![]()
dengan ![]() dan
dan ![]() . Jelas bahwa
. Jelas bahwa ![]() .
.
Akan digunakan induksi matematika untuk membuktikan persamaan (2) memiliki solusi bulat.
- Basis induksi:
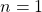 . Persamaan (2) menjadi
. Persamaan (2) menjadi 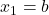 atau
atau 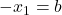 . Diperoleh
. Diperoleh 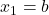 atau
atau 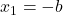 merupakan solusi, dan solusi ini tidak berisi parameter.
merupakan solusi, dan solusi ini tidak berisi parameter. - Langkah induksi: Diasumsikan persamaan (2) dengan
 variabel memiliki solusi bulat. Akan dibuktikan bahwa persamaan (1) dengan
variabel memiliki solusi bulat. Akan dibuktikan bahwa persamaan (1) dengan 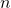 variabel memiliki solusi bulat. Misalkan
variabel memiliki solusi bulat. Misalkan 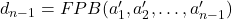 . Diperoleh bahwa setiap solusi bulat dari persamaan (2) memenuhi
. Diperoleh bahwa setiap solusi bulat dari persamaan (2) memenuhi
![Rendered by QuickLaTeX.com \[ a'_1x_1+a'_2x_2+\cdots+a'_n x_n\equiv b'\pmod{d_{n-1}}, \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-77314dd00aadd01cc2ee74831632ecd5_l3.png)
(3)
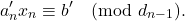
Dengan mengalikan kedua ruas pada persamaan (2) dengan
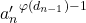 dan menggunakan fakta bahwa
dan menggunakan fakta bahwa 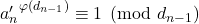 , diperoleh
, diperoleh![Rendered by QuickLaTeX.com \[ x_n\equiv c\pmod{d_{n-1}}, \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-7780c2a63900726c34032f330164b167_l3.png)
dengan
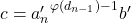 . Artinya,
. Artinya, 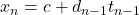 untuk suatu bilangan bulat
untuk suatu bilangan bulat 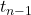 . Dengan mensubstitusi
. Dengan mensubstitusi 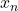 ke persamaan (2), diperoleh
ke persamaan (2), diperoleh![Rendered by QuickLaTeX.com \[ a'_1x_1+\cdots+a'_{n-1}x_{n-1}=b-a'_nc-a'_nd_{n-1}t_{n-1}. \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-881b916ec9b23d4c25d7215a1cc240dc_l3.png)
Hal ini berarti,
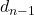 habis membagi
habis membagi 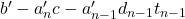 atau yang ekuivalen dengan
atau yang ekuivalen dengan 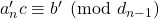 , sebab
, sebab 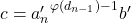 . Akibatnya, dengan membagi kedua ruas persamaan terakhir dengan
. Akibatnya, dengan membagi kedua ruas persamaan terakhir dengan 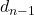 , diperoleh
, diperoleh
(4)
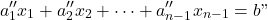
dengan
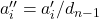 untuk
untuk 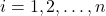 dan
dan 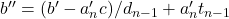 . Karena
. Karena 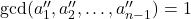 , maka sesuai asumsi induksi, persamaan (4) memiliki solusi bulat dan solusinya dapat ditulis ke dalam
, maka sesuai asumsi induksi, persamaan (4) memiliki solusi bulat dan solusinya dapat ditulis ke dalam  parameter. Jika pada solusi tersebut ditambahkan
parameter. Jika pada solusi tersebut ditambahkan 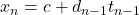 , diperoleh persamaan (2) memiliki solusi bulat dan solusinya dapat ditulis ke dalam
, diperoleh persamaan (2) memiliki solusi bulat dan solusinya dapat ditulis ke dalam  parameter.
parameter.
Terbukti bahwa persamaan (2) memiliki solusi bulat dan solusinya dapat ditulis ke dalam ![]() parameter.
parameter.
[/learn_more]
Contoh:
Selidiki apakah masing-masing persamaan berikut memiliki solusi bilangan bulat ![]() ? Jika ya, tentukan salah satu solusinya.
? Jika ya, tentukan salah satu solusinya.
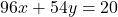 .
.-
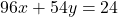 .
.
Solusi:
Pertama-tama, akan dicari ![]() . Salah satu cara yang dapat digunakan adalah dengan menggunakan algoritma Euclid. Berdasarkan algoritma Euclid,
. Salah satu cara yang dapat digunakan adalah dengan menggunakan algoritma Euclid. Berdasarkan algoritma Euclid,
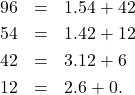
Jadi, ![]() .
.
- Karena
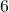 tidak habis membagi
tidak habis membagi 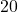 , berdasarkan Teorema ??, persamaan
, berdasarkan Teorema ??, persamaan 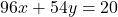 tidak memiliki solusi bulat.
tidak memiliki solusi bulat. - Karena
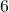 habis membagi
habis membagi 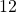 , berdasarkan Teorema ?? persamaan
, berdasarkan Teorema ?? persamaan 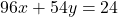 memiliki solusi bulat. Salah satu solusinya dapat dicari dengan menggunakan algoritma Euclid. Diperhatikan bahwa
memiliki solusi bulat. Salah satu solusinya dapat dicari dengan menggunakan algoritma Euclid. Diperhatikan bahwa
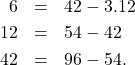
Diperoleh
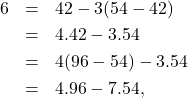
sehingga didapat
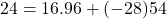 . Jadi,
. Jadi, 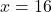 dan
dan 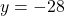 memenuhi persamaan
memenuhi persamaan 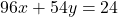 .
.
Salah satu akibat langsung dari Teorema 1 adalah jaminan bahwa solusi persamaan 1 ada ketika faktor persekutuan terbesar dari koefisien-koefisien pada setiap variabel adalah 1.
Akibat 1.
[box] Jika pada persamaan (1) berlaku ![]() , maka persamaan tersebut memiliki solusi bulat.[/box]
, maka persamaan tersebut memiliki solusi bulat.[/box]
Setelah mengetahui eksistensi solusi bulat persamaan Diophantine linear, pertanyaan selanjutnya adalah bagaimana mencari seluruh solusi bulat persamaan tersebut. Secara umum, tidak terdapat formula khusus untuk mencari solusinya. Namun, untuk persamaan Diophantine linear dengan dua variabel, semua solusi bulat dapat diperoleh dengan memanfaatkan Teorema ?? berikut.
[box] Diberikan ![]() dan
dan ![]() bilangan bulat dengan sifat
bilangan bulat dengan sifat ![]() habis membagi
habis membagi ![]() . Jika
. Jika ![]() merupakan solusi bulat dari persamaan
merupakan solusi bulat dari persamaan
![]()
maka setiap solusi bulat dari persamaan tersebut dinyatakan dalam bentuk
![]()
untuk suatu bilangan bulat ![]() .[/box]
.[/box]
[learn_more caption=”Bukti:” state=”open”]
Karena ![]() merupakan solusi bulat dari persamaan
merupakan solusi bulat dari persamaan ![]() , berlaku
, berlaku ![]() . Diambil sebarang
. Diambil sebarang ![]() solusi bulat persamaan
solusi bulat persamaan ![]() . Diperoleh
. Diperoleh
![]()
Dengan membagi kedua ruas persamaan tersebut dengan ![]() , diperoleh
, diperoleh
![]()
dengan ![]() dan
dan ![]() di mana
di mana ![]() . Perhatikan bahwa
. Perhatikan bahwa ![]() habis membagi ruas kiri persamaan terakhir. Akibatnya,
habis membagi ruas kiri persamaan terakhir. Akibatnya, ![]() juga habis membagi
juga habis membagi ![]() . Karena
. Karena ![]() , diperoleh
, diperoleh ![]() habis membagi
habis membagi ![]() . Artinya, terdapat bilangan bulat
. Artinya, terdapat bilangan bulat ![]() dengan sifat
dengan sifat ![]() atau
atau ![]() . Dengan mensubstitusi nilai
. Dengan mensubstitusi nilai ![]() ke persamaan terakhir, diperoleh
ke persamaan terakhir, diperoleh ![]() . Terbukti.
. Terbukti.
[/learn_more]
Teorema ?? juga dapat dimanfaatkan untuk mencari solusi bulat persamaan Diophantine linear atas tiga variabel atau lebih.
Contoh:
Tentukan semua tripel bilangan bulat (![]() ) yang memenuhi persamaan
) yang memenuhi persamaan ![]() .
.
Solusi:
Persamaan tersebut ekuivalen dengan ![]() . Misalkan
. Misalkan ![]() . Diperoleh
. Diperoleh
![]()
Perhatikan bahwa ![]() merupakan salat satu solusi bulat persamaan tersebut. Berdasarkan Teorema ??, diperoleh
merupakan salat satu solusi bulat persamaan tersebut. Berdasarkan Teorema ??, diperoleh ![]() dan
dan ![]() untuk suatu bilangan bulat
untuk suatu bilangan bulat ![]() . Dengan demikian, solusi dari persamaan tersebut adalah
. Dengan demikian, solusi dari persamaan tersebut adalah
![]()
dengan ![]() dan
dan ![]() merupakan bilangan bulat.
merupakan bilangan bulat.
Perhatikan bahwa Akibat ?? memberikan jaminan bahwa persamaan ![]() selalu memiliki solusi bulat untuk setiap bilangan asli
selalu memiliki solusi bulat untuk setiap bilangan asli ![]() jika
jika ![]() . Bagaimana jika solusi yang diinginkan adalah bilangan bulat non-negatif. Secara umum, terdapat ada tak berhingga bilangan asli
. Bagaimana jika solusi yang diinginkan adalah bilangan bulat non-negatif. Secara umum, terdapat ada tak berhingga bilangan asli ![]() sehingga persamaan tersebut memiliki solusi bulat non-negatif. Teorema Frobenius berikut memberikan banyaknya bilangan asli
sehingga persamaan tersebut memiliki solusi bulat non-negatif. Teorema Frobenius berikut memberikan banyaknya bilangan asli ![]() yang menyebabkan persamaan
yang menyebabkan persamaan ![]() tidak memiliki solusi bulat non-negatif.
tidak memiliki solusi bulat non-negatif.
Teorema [Teorema Frobenius]
[box] Diberikan bilangan bulat positif ![]() dan
dan ![]() dengan
dengan ![]() . Banyaknya bilangan bulat positif
. Banyaknya bilangan bulat positif ![]() yang menyebabkan persamaan
yang menyebabkan persamaan ![]() tidak memiliki solusi bulat non-negatif adalah
tidak memiliki solusi bulat non-negatif adalah ![]() [/box].
[/box].
[learn_more caption=”Bukti:” state=”open”]
Katakan bilangan bulat positif ![]() “baik” jika persamaan
“baik” jika persamaan ![]() tidak memiliki solusi bulat non-negatif. Perhatikan susunan berikut:
tidak memiliki solusi bulat non-negatif. Perhatikan susunan berikut:
![Rendered by QuickLaTeX.com \[ \begin{array}{ccccccc} 0&1&2&\ldots&\ell&\ldots&a-1\\ a&a+1&a+2&\ldots&a+\ell&\ldots&2a-1\\ 2a&2a+1&2a+2&\ldots&2a+\ell&\ldots&3a-1\\ \ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots \end{array} \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-45cb90f2202c91f1e2da87c3d994e671_l3.png)
di mana setiap kolom membentuk barisan artimatika dengan beda ![]() .
.
Jelas bahwa setiap kelipatan dari ![]() baik.
baik.
Perhatikan bahwa jika ada dua kelipatan dari ![]() , katakan
, katakan ![]() dan
dan ![]() dengan
dengan ![]() , berada pada kolom yang sama, maka kedua bilangan tersebut sama. Apabila kedua bilangan tersebut terletak pada kolom yang sama, maka berlaku
, berada pada kolom yang sama, maka kedua bilangan tersebut sama. Apabila kedua bilangan tersebut terletak pada kolom yang sama, maka berlaku ![]() . Akibatnya
. Akibatnya ![]() . Karena
. Karena ![]() , maka
, maka ![]() . Karena
. Karena ![]() , maka
, maka ![]() , sehingga
, sehingga ![]() .
.
Akan ditunjukkan bahwa setiap bilangan yang berada di atas (dalam satu kolom) salah satu kelipatan ![]() ,
, ![]() , tidak baik. Perhatikan bahwa sebarang bilangan yang berada di atas
, tidak baik. Perhatikan bahwa sebarang bilangan yang berada di atas ![]() berbentuk
berbentuk ![]() untuk suatu bilangan bulat positif
untuk suatu bilangan bulat positif ![]() . Jika
. Jika ![]() baik, maka
baik, maka ![]() untuk suatu bilangan bulat non-negatif
untuk suatu bilangan bulat non-negatif ![]() dan
dan ![]() . Diperoleh
. Diperoleh ![]() , yang berarti
, yang berarti ![]() . Akibatnya,
. Akibatnya, ![]() . Di sisi lain, dua bilangan yang terletak pada kolom yang sama kongruen dalam modulo
. Di sisi lain, dua bilangan yang terletak pada kolom yang sama kongruen dalam modulo ![]() . Diperoleh
. Diperoleh ![]() , yang berarti
, yang berarti ![]() . Karena
. Karena ![]() , maka
, maka ![]() , suatu kontradiksi.
, suatu kontradiksi.
Perhatikan bahwa jika ![]() baik, maka
baik, maka ![]() juga baik untuk setiap bilangan asli
juga baik untuk setiap bilangan asli ![]() . Dengan demikian, banyaknya bilangan asli yang tidak baik sama dengan banyaknya bilangan yang berada di atas (dalam satu kolom) bilangan berbentuk
. Dengan demikian, banyaknya bilangan asli yang tidak baik sama dengan banyaknya bilangan yang berada di atas (dalam satu kolom) bilangan berbentuk ![]() ,
, ![]() . Diperhatikan bahwa pada kolom ke-
. Diperhatikan bahwa pada kolom ke-![]() , terdapat
, terdapat ![]() bilangan yang berada di atas
bilangan yang berada di atas ![]() . Akibatnya diperoleh banyaknya bilangan yang tidak baik adalah
. Akibatnya diperoleh banyaknya bilangan yang tidak baik adalah
![Rendered by QuickLaTeX.com \[ \sum_{v=0}^{a-1}\sum_{j=0}^{a-1}\frac{vb-j}{a}=\frac{(a-1)(b-1)}{2}. \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-3eb56c84e197754a27a038c2f3801922_l3.png)
[/learn_more]
Berdasarkan bukti pada Teorema Frobenius di atas, diketahui bahwa bilangan asli terbesar ![]() yang menyebabkan persamaan
yang menyebabkan persamaan ![]() tidak memiliki solusi bulat non-negatif adalah
tidak memiliki solusi bulat non-negatif adalah ![]() . Dengan demikian, diperoleh syarat cukup untuk
. Dengan demikian, diperoleh syarat cukup untuk ![]() agar persamaan
agar persamaan ![]() memiliki solusi bulat non-negatif sebagai berikut.
memiliki solusi bulat non-negatif sebagai berikut.
Akibat 2
[box] Diberikan bilangan bulat positif ![]() dan
dan ![]() yang saling prima. Persamaan
yang saling prima. Persamaan
![]()
tidak memiliki solusi bulat non-negatif untuk ![]() . Jika
. Jika ![]() , maka persamaan tersebut memiliki solusi bulat non-negatif
, maka persamaan tersebut memiliki solusi bulat non-negatif ![]() dan
dan ![]() . [\box]
. [\box]
Selanjutnya, Pembaca dapat mengerjakan soal-soal berikut sebagai latihan.
- Tentukan semua solusi bulat persamaan-persamaan linear Diophantine berikut.
a.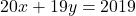 .
.
b.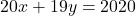 .
.
c.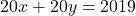 .
.
d.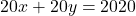 .
. - Tentukan semua solusi bulat
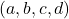 dari persamaan
dari persamaan
![Rendered by QuickLaTeX.com \[ (6a+9b)(7c+8d)=3. \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-4961d78f8cbcfe10861d7b59fef35435_l3.png)
- Tentukan semua bilangan bulat
 dan
dan 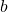 sehingga
sehingga 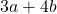 habis membagi 2020.
habis membagi 2020. - Tunjukkan bahwa luas segitiga dengan titik-titik sudut
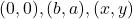 adalah
adalah
![Rendered by QuickLaTeX.com \[ \frac{|ax-by|}{2}. \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-be46e6f25805243a9f3a57c2bd3a4ccc_l3.png)
- Tentukan bilangan bulat positif
 dan
dan 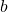 dengan sifat banyaknya bilangan bulat positif
dengan sifat banyaknya bilangan bulat positif 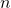 yang tidak dapat dinyatakan dalam bentuk
yang tidak dapat dinyatakan dalam bentuk 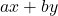 untuk suatu bilangan bulat non-negatif
untuk suatu bilangan bulat non-negatif 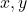 adalah 35 dan salah satu bilangan tersebut adalah 58.
adalah 35 dan salah satu bilangan tersebut adalah 58. - Tentukan bilangan bulat positif terbesar yang tidak dapat dinyatakan dalam bentuk
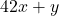 untuk suatu bilangan bulat positif
untuk suatu bilangan bulat positif 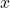 dan
dan 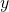 dengan
dengan 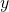 komposit.
komposit.
1 Comment
Puji Erpe · April 12, 2021 at 10:31 am
Waah, berapa tahun lalu ya belajar materi ini?
Terimakasih atas materinya, jadi mengingat kembali.