Sistem bilangan asli sudah dikenalkan ke masyarakat umum sejak pendidikan di tingkat sekolah dasar (SD). Pada pendidikan di tingkat SD ini, siswa sudah dikenalkan bilangan 1, 2 ,3 dan seterusnya. Namun demikian, siswa belum diajarkan bagaimana proses pembentukan bilangan-bilangan tersebut. Pada artikel ini akan dijelaskan bagaimana proses pembentukan sistem bilangan asli.
Mempelajari sistem bilangan asli merupakan salah satu tahapan yang perlu dilakukan sebelum mempelajari sistem bilangan bulat.
Definisi 1
[box]
Diketahui ![]() himpunan yang memuat
himpunan yang memuat ![]() dan dilengkapi operasi biner “+” pada
dan dilengkapi operasi biner “+” pada ![]() . Jika
. Jika ![]() memenuhi:
memenuhi:
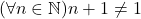
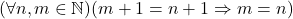
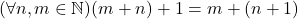
- Untuk setiap
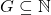 , jika4.1
, jika4.1 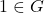 dan4.2
dan4.2 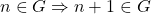 ,
,
maka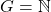 ,
,
maka ![]() disebut sistem bilangan asli (himpunan bilangan asli). Selanjutnya untuk setiap
disebut sistem bilangan asli (himpunan bilangan asli). Selanjutnya untuk setiap ![]() disebut bilangan asli.
disebut bilangan asli.
[/box]
Dari sistem aksioma di atas dapat dikonstruksi:
![]()
Teorema 1
![]()
[learn_more caption=”Bukti:” state=”open”]
Dari definisi 1
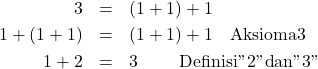
[/learn_more]
Sebagai latihan, pembaca dapat membuktikan pernyataan-pernyataan berikut ini.
Berdasarkan aksiomatika dapat diturunkan teorema berikut ini.
Teorema 2
Untuk setiap ![]() berlaku
berlaku ![]() .
.
[learn_more caption=”Bukti:” state=”open”]
Dibentuk ![]() . jelas
. jelas ![]() . Berdasar A (Aksioma) 1,
. Berdasar A (Aksioma) 1, ![]() , sehingga
, sehingga ![]() .
.
Misalkan ![]() , yaitu
, yaitu ![]() . Namun berdasarkan A2,
. Namun berdasarkan A2, ![]() , sehingga
, sehingga ![]() ; dan sesuai A4,
; dan sesuai A4, ![]() . Akibatnya untuk
. Akibatnya untuk
semua ![]() berlaku
berlaku ![]() . Jadi
. Jadi ![]() untuk setiap
untuk setiap ![]() .
. ![]()
[/learn_more]
Teorema 3
Untuk setiap ![]() berlaku
berlaku ![]() .
.
[learn_more caption=”Bukti:” state=”open”]
Diambil sebarang ![]() . Dibentuk
. Dibentuk ![]() . Berdasarkan Teorema 2
. Berdasarkan Teorema 2 ![]() . Dimisalkan
. Dimisalkan ![]() . Hal ini berarti
. Hal ini berarti ![]() . Andai
. Andai ![]() akan berakibat
akan berakibat ![]() , sehingga menurut A2
, sehingga menurut A2 ![]() . Kontradiksi dengan hipotesa induksi. Jadi
. Kontradiksi dengan hipotesa induksi. Jadi ![]() dan menurut A4 berakibat sifat terbukti.
dan menurut A4 berakibat sifat terbukti. ![]()
[/learn_more]
Sifat berikutnya yang dapat diturunkan berdasarkan sistem aksiomatika himpunan ![]() beserta operasi “
beserta operasi “![]() ” adalah sifat asosiatif.
” adalah sifat asosiatif.
Teorema 4
Untuk setiap ![]() memenuhi
memenuhi ![]() .
.
[learn_more caption=”Bukti:” state=”open”]
Diambil sebarang ![]() . Pembuktian dengan induksi matematika dikenakan pada
. Pembuktian dengan induksi matematika dikenakan pada ![]() dengan membentuk
dengan membentuk
![]()
Berdasarkan A3, diperoleh ![]() . Dimisalkan benar untuk
. Dimisalkan benar untuk ![]() , yaitu
, yaitu ![]() .
.
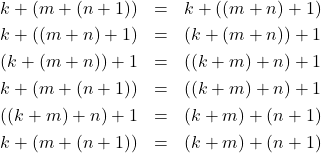
Akibatnya ![]() . Sesuai A4,
. Sesuai A4, ![]() , sehingga untuk setiap
, sehingga untuk setiap ![]() ,
, ![]() .
. ![]()
[/learn_more]
Berdasarkan Teorema 4, hasil jumlahan ![]() sebanyak
sebanyak ![]() suku
suku
![]()
cukup ditulis ![]() .
.
Teorema 5
Diketahui ![]() jumlahan bilangan 1 sebanyak
jumlahan bilangan 1 sebanyak ![]() suku dan
suku dan ![]() . jumlahan bilangan
. jumlahan bilangan ![]() sebanyak
sebanyak ![]() suku. Jika banyaknya
suku. Jika banyaknya ![]() penyusun
penyusun ![]() lebih sedikit daripada di
lebih sedikit daripada di ![]() , maka
, maka ![]() .
.
[learn_more caption=”Bukti:” state=”open”]
Karena ![]() untuk suatu
untuk suatu ![]() , dengan
, dengan ![]() . Akibatnya
. Akibatnya ![]() .
. ![]()
Untuk selanjutnya ![]() ditulis
ditulis ![]() . Misalkan
. Misalkan
![]()
Jelas ![]() dan jika
dan jika ![]() , berlaku
, berlaku
![]()
Sesuai Aksioma 4 berlaku ![]() .
. ![]() .
.
[/learn_more]
Sifat berikutnya yang berlaku terhadap operasi “![]() ” adalah komutatif. Untuk itu diperlukan lemma berikut ini sebagai landasan.
” adalah komutatif. Untuk itu diperlukan lemma berikut ini sebagai landasan.
Lemma 1
Untuk setiap ![]() ,
, ![]() .
.
[learn_more caption=”Bukti:” state=”open”]
Dibentuk ![]() . Jelas
. Jelas ![]() . Karena
. Karena ![]() , maka
, maka ![]() . Selanjutnya dimisalkan
. Selanjutnya dimisalkan ![]() , yang berarti
, yang berarti ![]() . Akibatnya
. Akibatnya ![]() , sehingga
, sehingga ![]() ; dan berdasarkan A4,
; dan berdasarkan A4, ![]() .
. ![]()
[/learn_more]
Teorema 6
Untuk setiap ![]() berlaku
berlaku ![]() .
.
[learn_more caption=”Bukti:” state=”open”]
Diambil sebarang ![]() . Dibentuk
. Dibentuk ![]() . Jelas
. Jelas ![]() . Selain itu menurut Lemma 1,
. Selain itu menurut Lemma 1,
![]() . Selanjutnya dimisalkan
. Selanjutnya dimisalkan ![]() . Berarti
. Berarti ![]() .
.
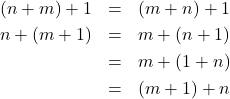
Akibatnya ![]() , sehingga menurut A4,
, sehingga menurut A4, ![]() . Dengan kata lain untuk setiap
. Dengan kata lain untuk setiap ![]() ,
, ![]() .
. ![]()
[/learn_more]
Teorema 7 [Sifat Kanselatif]
Dalam sistem bilangan ![]() berlaku sifat kanselatif kiri dan kanan:
berlaku sifat kanselatif kiri dan kanan:
- Untuk setiap
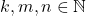 ,
, 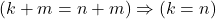
- Untuk setiap
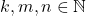 ,
, 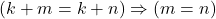
[learn_more caption=”Bukti:” state=”open”]
Hanya dibuktikan untuk 1. Sifat 2 dijadikan latihan. Bukti menggunakan kontraposisinya, yaitu
![]()
Diambil sebarang ![]() dan
dan ![]() , dengan
, dengan ![]() . Dibentuk
. Dibentuk ![]() . Karena
. Karena ![]() jelas
jelas ![]()
Dimisalkan ![]() , dengan kata lain
, dengan kata lain ![]() . Akibatnya
. Akibatnya
![]()
sehingga ![]() . Sesuai A4, dapat disimpulkan
. Sesuai A4, dapat disimpulkan ![]() , sehingga untuk setiap
, sehingga untuk setiap ![]() , jika
, jika ![]() , maka
, maka ![]() untuk setiap
untuk setiap
![]() .
. ![]()
[/learn_more]
Latihan
- Teorema 7, bagian 2.
- Untuk setiap
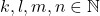 berlaku
berlaku 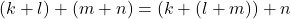 .
.
0 Comments