Berdasarkan operasi penjumlahan pada ![]() selanjutnya dikonstruksi operasi perkalian dua bilangan asli. Operasi ini muncul dari penjumlahan secara berulang bilangan asli yang memunculkan pemetaan biner pada
selanjutnya dikonstruksi operasi perkalian dua bilangan asli. Operasi ini muncul dari penjumlahan secara berulang bilangan asli yang memunculkan pemetaan biner pada ![]() sperti dalam teorema berikut ini.
sperti dalam teorema berikut ini.
Teorema 1
Pada himpunan bilangan asli ![]() terdapat dengan tunggal pemetaan
terdapat dengan tunggal pemetaan ![]() yang memenuhi
yang memenuhi
![]()
untuk setiap ![]() . Untuk selanjutnya ditulis
. Untuk selanjutnya ditulis ![]() .
.
[learn_more caption=”Bukti:” state=”open”]
Terhadap pengaitan ![]() dengan
dengan
![]()
untuk ![]() ,
, ![]() . Misalkan untuk sebarang
. Misalkan untuk sebarang ![]() berlaku
berlaku ![]() . Akibatnya
. Akibatnya
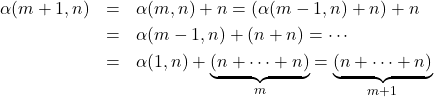
Untuk sebarang ![]() jika
jika ![]() ,
, ![]() . Jika diketahui juga
. Jika diketahui juga ![]() dan diasumsikan
dan diasumsikan ![]() maka
maka
![]()
sehingga terbukti ![]() pemetaan. Bukti ketunggalan dijadikan latihan.
pemetaan. Bukti ketunggalan dijadikan latihan. ![]()
[/learn_more]
Contoh 1
Sebagai contoh diambil ![]() . Secara umum
. Secara umum
![]()
sebanyak ![]() suku.
suku.
Teorema 2
Untuk setiap ![]() berlaku
berlaku
![]()
Teorema 3
Untuk setiap ![]() berlaku:
berlaku:
- Distributif:
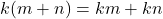 dan
dan 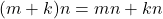
- Assosiatif:
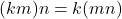
- Komutatif:
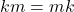
- Kanselatif: Jika
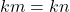 , maka
, maka 
[learn_more caption=”Bukti:” state=”open”]
- Diambil sebarang
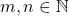 . Dibentuk
. Dibentuk
![Rendered by QuickLaTeX.com \[ G = \{ k \in \mathbb{N}~|~k(m + n) = km + kn \} \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-304737ff485660861fa5f6126ca43ec9_l3.png)
Jelas
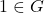 . Diasumsikan
. Diasumsikan 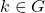 . Berarti
. Berarti 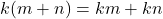 sehingga
sehingga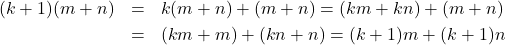
Akibatnya
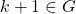 , sehingga
, sehingga 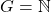 .Dibentuk
.Dibentuk 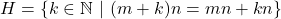 . Karena
. Karena 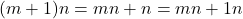 , berarti
, berarti 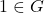 . Diasunsikan
. Diasunsikan 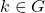 . Akibatnya
. Akibatnya 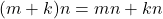 , sehingga
, sehingga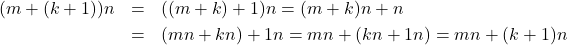
Jadi
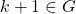 . Dengan kata lain
. Dengan kata lain 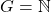 .
. - Diambil sebarang
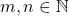 sebarang. Dibentuk
sebarang. Dibentuk
![Rendered by QuickLaTeX.com \[ G = \{ k \in \mathbb{N}~|~(km)n = k(mn) \} \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-497a7a3023d6701dccea525387801648_l3.png)
Untuk
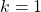 berlaku
berlaku 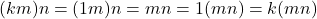 . Akibatnya
. Akibatnya 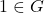 . Dimisalkan
. Dimisalkan 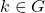 . Karena distributif kanan berlaku
. Karena distributif kanan berlaku![Rendered by QuickLaTeX.com \[ ((k + 1)m)n = (km + 1m)n = (km)n + (1m)n = k(mn) + mn = (k + 1)(mn) \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-65ee7b38fbf8140d287f7e90832a1ba7_l3.png)
Berarti
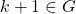 , sehingga
, sehingga 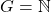 .
. - Untuk sebarang
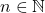 berlaku
berlaku 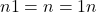 , sebab: Untuk
, sebab: Untuk 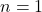
![Rendered by QuickLaTeX.com \[ n1 = 1\cdot 1 = 1 = n = 1n \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-4cf9bedc12816fdec8255b91dcde1c72_l3.png)
Misalkan
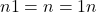 . Akibatnya
. Akibatnya 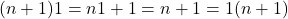 .
.
Selanjutnya dimisalkan untuk sebarang
untuk sebarang 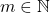 . Akibatnya dengan menggunakan sifat distributif kiri
. Akibatnya dengan menggunakan sifat distributif kiri![Rendered by QuickLaTeX.com \[ (m + 1)n = mn + n = nm + n1 = n(m + 1)\]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-0c7cff72c16e7e04adb9d887168d0d65_l3.png)
sehingga
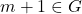 . Jadi komutatif berlaku.
. Jadi komutatif berlaku. - Diketahui
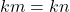 . Diandaikan
. Diandaikan 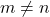 . Akibatnya terdapat
. Akibatnya terdapat 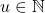 yang memenuhi
yang memenuhi 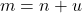 atau
atau 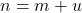 , sehingga
, sehingga
![Rendered by QuickLaTeX.com \[ kn = k(n + u) = kn + ku~~{\rm atau}~~km = k(m + u) = km + ku \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-0a793f9b7326480175674e107482a1c6_l3.png)
keduanya tidak mubgkin terjadi, karena
 . Jadi
. Jadi  .
. 
[/learn_more]
Teorema 4
Jika ![]() dan
dan ![]() bilangan asli,
bilangan asli, ![]() jika dan hanya jika
jika dan hanya jika ![]() .
.
[learn_more caption=”Bukti:” state=”open”]
Jika ![]() ,
, ![]() . Sebaliknya misalkan
. Sebaliknya misalkan ![]() . Andaikan
. Andaikan ![]() atau
atau ![]() . Akibatnya
. Akibatnya ![]() . Kontradiksi. Begitu juga jika
. Kontradiksi. Begitu juga jika ![]() dan
dan ![]() . Sedangkan jika
. Sedangkan jika ![]() , maka terdapat
, maka terdapat ![]() sehingga
sehingga ![]() dan
dan ![]() . Dapat disimpulkan
. Dapat disimpulkan ![]() . Kontradiksi.
. Kontradiksi. ![]() .
.
[/learn_more]
Berdasarkan sifat komutatif operasi perkalian pada ![]() , semua sifat yang berlaku untuk perkalian dengan elemen dari sisi sebelah kiri juga berlaku untuk perkalian dengan elemen di sebelah kanan.
, semua sifat yang berlaku untuk perkalian dengan elemen dari sisi sebelah kiri juga berlaku untuk perkalian dengan elemen di sebelah kanan.
Teorema 5
Diketahui ![]() .
.
- Jika
 , maka
, maka  dan
dan 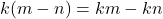
- Jika
 dan
dan 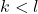 , maka
, maka 
- Jika
 , maka
, maka 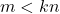
[learn_more caption=”Bukti:” state=”open”]
Karena ![]() maka dapat ditemukan
maka dapat ditemukan ![]() yang memenuhi
yang memenuhi ![]() .
.
- Akibatnya
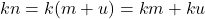 . Tentu saja
. Tentu saja 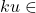 , sehingga
, sehingga  dan
dan 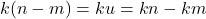 .
. - Karena
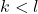 , maka terdapat
, maka terdapat  yang memenuhi
yang memenuhi 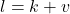 .
.
![Rendered by QuickLaTeX.com \[ nl = (m + u)(k + v) = mk + (uk + mv + uv) \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-74ed4b9240c602b2b7d6d5463b247ebe_l3.png)
Hal ini berakibat
 .
. - Merupakan akibat dari kasus 1 dan 2.

[/learn_more]
0 Comments