Apakah Anda sudah pernah mendengar kata order? Dimanakah anda menjumpai kata tersebut?
Kata order dapat ditemui salah satunya pada pembahasan mengenai strukrut aljabar, khususnya teori grup dan teori ring. Order dari suatu elemen a di grup atau ring adalah bilangan asli terkecil sehingga a dipangkatkan dengan bilangan tersebut hasilnya adalah elemen identitas. Pada artikel ini akan dibahas mengenai order dari suatu bilangan.
Order dari Suatu Bilangan
Diberikan bilangan asli relatif prima ![]() dan
dan ![]() . Apakah selalu terdapat bilangan asli
. Apakah selalu terdapat bilangan asli ![]() sehingga
sehingga ![]() ? Artikel ini akan menyelidiki sifat-sifat bilangan
? Artikel ini akan menyelidiki sifat-sifat bilangan ![]() yang memenuhi kondisi tersebut.
yang memenuhi kondisi tersebut.
Tinjau himpunan ![]() di modulo
di modulo ![]() . Jelas bahwa hanya terdapat sebanyak
. Jelas bahwa hanya terdapat sebanyak ![]() (berhingga) residu di modulo
(berhingga) residu di modulo ![]() . Akibatnya, pasti terdapat dua anggota
. Akibatnya, pasti terdapat dua anggota ![]() yang kongruen di modulo
yang kongruen di modulo ![]() , sebut
, sebut ![]() dengan
dengan ![]() . Jadi,
. Jadi, ![]() sehingga terbukti bahwa selalu terdapat bilangan asli
sehingga terbukti bahwa selalu terdapat bilangan asli ![]() yang memenuhi
yang memenuhi ![]() .
.
Selanjutnya kita akan menyelidiki sifat-sifat bilangan asli terkecil yang memenuhi sifat tersebut.
Definisi
Diberikan bilangan asli ![]() dan
dan ![]() dengan
dengan ![]() . Bilangan asli
. Bilangan asli ![]() disebut sebagai \textbf{order} dari
disebut sebagai \textbf{order} dari ![]() modulo
modulo ![]() , atau dituliskan
, atau dituliskan ![]() apabila
apabila ![]() merupakan bilangan asli terkecil yang memenuhi
merupakan bilangan asli terkecil yang memenuhi ![]() .
.
Sebagai contoh, perhatikan barisan ![]() di modulo 7 berikut
di modulo 7 berikut
![]()
Dapat dilihat bahwa order dari 2 modulo 7 adalah 3 atau dituliskan ![]() . Perhatikan bahwa pula bahwa apabila
. Perhatikan bahwa pula bahwa apabila ![]() , maka
, maka ![]() haruslah merupakan kelipatan 3 (ordernya). Sifat yang cukup intuitif tersebut dibahas pada teorema berikut.
haruslah merupakan kelipatan 3 (ordernya). Sifat yang cukup intuitif tersebut dibahas pada teorema berikut.
Teorema 1.
[box] Diberikan bilangan asli ![]() dan
dan ![]() dengan
dengan ![]() . Jika
. Jika ![]() , maka untuk sebarang bilangan asli
, maka untuk sebarang bilangan asli ![]() yang memenuhi
yang memenuhi ![]() , berlaku
, berlaku ![]() . [/box]
. [/box]
[learn_more caption=”Bukti:” state=”open”]
Menurut algoritma pembagian, terdapat bilangan bulat ![]() dan
dan ![]() yang memenuhi
yang memenuhi ![]() dan
dan ![]() . Perhatikan bahwa
. Perhatikan bahwa
![]()
Akibatnya, ![]() . Apabila
. Apabila ![]() , maka karena
, maka karena ![]() , diperoleh suatu kontradiksi dengan fakta bahwa
, diperoleh suatu kontradiksi dengan fakta bahwa ![]() merupakan bilangan asli terkecil sehingga
merupakan bilangan asli terkecil sehingga ![]() . Jadi,
. Jadi, ![]() dan disimpulkan bahwa
dan disimpulkan bahwa ![]() .
.
[/learn_more]
Akibat 2.
[box] Diberikan bilangan asli ![]() . Berikut adalah beberapa akibat dari Teorema 1.
. Berikut adalah beberapa akibat dari Teorema 1.
- Jika
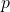 adalah bilangan prima, maka
adalah bilangan prima, maka 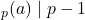 .
. - Jika
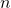 adalah bilangan asli yang relatif prima dengan
adalah bilangan asli yang relatif prima dengan  , maka
, maka 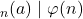 .
. - Jika
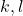 dan
dan 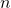 adalah bilangan asli serta
adalah bilangan asli serta 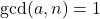 dan
dan 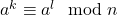 , maka
, maka 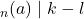 . [/box]
. [/box]
Teorema 3
[box] Untuk sebarang bilangan asli ![]() dan
dan ![]() dengan
dengan ![]() , berlaku
, berlaku
![]()
[/box]
[learn_more caption=”Bukti:” state=”open”]
Jelas bahwa ![]() pasti membagi
pasti membagi ![]() dan
dan ![]() sehingga
sehingga
![]()
Selanjutnya, diambil sebarang bilangan asli ![]() yang membagi
yang membagi ![]() dan
dan ![]() . Jelas bahwa
. Jelas bahwa ![]() sehingga
sehingga ![]() dan
dan ![]() punya inverse di modulo
punya inverse di modulo ![]() . Menurut Bezout, terdapat bilangan bulat
. Menurut Bezout, terdapat bilangan bulat ![]() dan
dan ![]() sehingga
sehingga ![]() . Jadi
. Jadi
![]()
sehingga ![]() . Karena ini berlaku untuk setiap
. Karena ini berlaku untuk setiap ![]() pembagi persekutuan
pembagi persekutuan ![]() dan
dan ![]() , jika dipilih
, jika dipilih ![]() , maka didapat
, maka didapat
![]()
[/learn_more]
Contoh
Contoh 1
[AIME 2001]
Banyaknya kelipatan 1001 yang dapat dinyatakan dalam bentuk ![]() di mana
di mana ![]() dan
dan ![]() adalah bilangan bulat dan
adalah bilangan bulat dan ![]() adalah
adalah ![]()
Solusi:
Diperhatikan bahwa
![]()
Jadi, ![]() . Namun, karena
. Namun, karena ![]() , maka
, maka ![]() . Akibatnya, jika untuk suatu
. Akibatnya, jika untuk suatu ![]() dengan
dengan ![]() berlaku
berlaku ![]() , berlaku
, berlaku
![]()
Begitu pula sebaliknya. Apabila ![]() adalah pasangan di mana
adalah pasangan di mana ![]() dengan
dengan ![]() , pasti berlaku
, pasti berlaku ![]() . Akibatnya, cukup dihitung banyaknya
. Akibatnya, cukup dihitung banyaknya ![]() yang memenuhi
yang memenuhi ![]() dan
dan ![]() . Pembaca dipersilahkan untuk memverifikasi bahwa banyaknya pasangan tersebut adalah 784.
. Pembaca dipersilahkan untuk memverifikasi bahwa banyaknya pasangan tersebut adalah 784.
Contoh 2
Diberikan bilangan prima ![]() . Buktikan bahwa semua faktor prima
. Buktikan bahwa semua faktor prima ![]() lebih besar dari
lebih besar dari ![]() .
.
Solusi:
Misalkan ![]() adalah faktor prima
adalah faktor prima ![]() dan
dan ![]() . Diperoleh
. Diperoleh
![]()
Akibatnya, ![]() dan
dan ![]() . Karena
. Karena ![]() , maka
, maka ![]() atau
atau ![]() .
.
- Jika
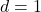 , diperoleh kontradiksi sebab
, diperoleh kontradiksi sebab 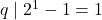 .
. - Jika
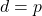 , diperoleh
, diperoleh 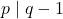 sehingga $q-1 \leq p \implies q > p
sehingga $q-1 \leq p \implies q > p
Terbukti.
0 Comments