Teorema kecil Fermat merupakan salah satu teori penting yang mendasari berbagai macam teorema penting lain di dalam teori bilangan. Pada tulisan ini akan dijelaskan isi dan bukti dari teorema kecil Fermat beserta contoh pengaplikasiannya. Selain itu, salah satu perumuman dari teorema kecil Fermat juga akan dibahas.
Teorema Kecil Fermat
Teorema 1 [Teorema Kecil Fermat]
[box] Jika ![]() bilangan prima, maka untuk setiap bilangan bulat positif
bilangan prima, maka untuk setiap bilangan bulat positif ![]() berlaku
berlaku ![]() . Lebih lanjut, jika
. Lebih lanjut, jika ![]() dan
dan ![]() saling relatif prima, maka berlaku
saling relatif prima, maka berlaku ![]() . [/box]
. [/box]
[learn_more caption=”Bukti:” state=”open”]
Cukup dibuktikan pernyataan kedua. Misalkan ![]() adalah bilangan bulat positif yang relatif prima dengan
adalah bilangan bulat positif yang relatif prima dengan ![]() . Perhatikan bahwa bilangan
. Perhatikan bahwa bilangan
![]()
masing-masing memiliki sisa yang berbeda dalam modulo ![]() . Akibatnya, diperoleh
. Akibatnya, diperoleh
![]()
Karena ![]() , diperoleh
, diperoleh
![]()
[/learn_more]
Secara umum, teorema ini sering dimanfaatkan dalam mencari sisa pembagian suatu bilangan oleh suatu bilangan prima.
Contoh:
Tentukan sisa pembagian ![]() oleh 13.
oleh 13.
Solusi:
Perhatikan bahwa 13 merupakan bilangan prima dan ![]() . Diperoleh
. Diperoleh
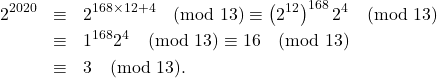
Dengan demikian, sisa pembagiannya adalah ![]() .
.
Contoh:
Diberikan bilangan prima ![]() . Tunjukkan bahwa
. Tunjukkan bahwa
![]()
habis dibagi oleh ![]() .
.
Solusi:
Diperhatikan bahwa
![Rendered by QuickLaTeX.com \[ \underbrace{11\ldots1}_{(p-1)\ \text{kali}}=\frac{10^{p-1}-1}{9}. \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-241e017d89740c542a69e04d2886d464_l3.png)
Karena ![]() dan
dan ![]() saling relatif prima, berdasarkan Teorema Kecil Fermat diperoleh
saling relatif prima, berdasarkan Teorema Kecil Fermat diperoleh ![]() habis membagi
habis membagi ![]() . Akibatnya,
. Akibatnya,
![]()
habis dibagi oleh ![]() .
.
Generalisasi: Teorema Euler
Terdapat berbagai macam perumuman dari teorema kecil Fermat, salah satunya dalah Teorema Euler. Sebelum membahas teorema tersebut, akan dibahas mengenai fungsi Euler terlebih dahulu. Fungsi Euler adalah fungsi ![]() definisikan sebagai berikut: untuk setiap bilangan bulat positif
definisikan sebagai berikut: untuk setiap bilangan bulat positif ![]() ,
, ![]() adalah banyaknya bilangan bulat positif
adalah banyaknya bilangan bulat positif ![]() dan relatif prima dengan
dan relatif prima dengan ![]() . Beberapa sifat dasar dari fungsi Euler diberikan dalam proposisi berikut.
. Beberapa sifat dasar dari fungsi Euler diberikan dalam proposisi berikut.
Proposisi 1
[box]
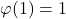 .
.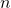 merupakan bilangan prima jika dan hanya jika
merupakan bilangan prima jika dan hanya jika 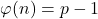
- Jika
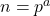 dengan
dengan 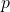 merupakan bilangan prima dan
merupakan bilangan prima dan  bilangan bulat positif, maka
bilangan bulat positif, maka 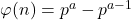 .[/box]
.[/box]
Selanjutnya akan diberikan formula untuk menghitung ![]() untuk setiap bilangan bulat positif
untuk setiap bilangan bulat positif ![]() .
.
Definisi:
Jelas bahwa untuk setiap ![]() , himpunan semua bilangan bulat positif yang kurang dari
, himpunan semua bilangan bulat positif yang kurang dari ![]() dan relatif prima dengan
dan relatif prima dengan ![]() adalah himpunan kelas residu tereduksi lengkap modulo
adalah himpunan kelas residu tereduksi lengkap modulo ![]() . Lebih lanjut, suatu himpunan kelas residu tereduksi lengkap modulo
. Lebih lanjut, suatu himpunan kelas residu tereduksi lengkap modulo ![]() memiliki sebanyak
memiliki sebanyak ![]() anggota.
anggota.
Proposisi 2
[box] Jika ![]() dan
dan ![]() bilangan bulat positif yang relatif prima, maka
bilangan bulat positif yang relatif prima, maka ![]() . [/box]
. [/box]
[learn_more caption=”Bukti:” state=”open”]
Disusun bilangan ![]() sebagai berikut:
sebagai berikut:
![Rendered by QuickLaTeX.com \[ \begin{array}{cccc} 1&2&\ldots&a\\ a+1&a+2&\ldots&2a\\ \vdots&\vdots&\vdots&\vdots\\ a(b-1)+1&a(b-1)+2&\ldots&ab. \end{array} \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-66c6550489ce7bdfc2f6d82543810616_l3.png)
Jelas bahwa di antara bilangan-bilangan ![]() terdapat
terdapat ![]() bilangan yang relatif prima dengan
bilangan yang relatif prima dengan ![]() . Di lain pihak, terdapat
. Di lain pihak, terdapat ![]() kolom yang mengandung bilangan-bilangan yang relatif prima dengan
kolom yang mengandung bilangan-bilangan yang relatif prima dengan ![]() . Karena setiap kolom merupakan himpunan kelas residu lengkap modulo
. Karena setiap kolom merupakan himpunan kelas residu lengkap modulo ![]() , maka terdapat tepat
, maka terdapat tepat ![]() bilangan pada masing-masing kolom yang relatif prima dengan
bilangan pada masing-masing kolom yang relatif prima dengan ![]() . Akibatnya, banyaknya bilangan yang relatif prima dengan
. Akibatnya, banyaknya bilangan yang relatif prima dengan ![]() pada susunan tersebut adalah
pada susunan tersebut adalah ![]() . Jadi,
. Jadi, ![]() .
.
[/learn_more]
Dengan mengkombinasikan Proposisi 1 dan Proposisi 2, diperoleh formula umum dari fungsi Euler sebagai berikut.
Teorema
[box] Diberikan bilangan bulat positif ![]() . Jika
. Jika ![]() faktorisasi prima dari
faktorisasi prima dari ![]() , maka
, maka
![]()
[/box]
Contoh:
Tunjukkan bahwa ada tak hingga banyaknya bilangan bulat positif ![]() dengan sifat
dengan sifat ![]() merupakan kelipatan 10.
merupakan kelipatan 10.
Solusi:
Diambil ![]() . Diperoleh
. Diperoleh ![]() yang merupakan kelipatan 10.
yang merupakan kelipatan 10.
Teorema Euler diberikan dalam teorema berikut.
Teorema 2
[box] Jika ![]() dan
dan ![]() bilangan bulat positif dengan
bilangan bulat positif dengan ![]() , maka
, maka ![]() .[box]
.[box]
[learn_more caption=”Bukti:” state=”open”]
Misalkan ![]() himpunan semua bilangan bulat positif yang kurang dari
himpunan semua bilangan bulat positif yang kurang dari ![]() dan relatif prima dengan
dan relatif prima dengan ![]() . Jelas bahwa
. Jelas bahwa ![]() merupakan himpunan kelas residu tereduksi lengkap modulo
merupakan himpunan kelas residu tereduksi lengkap modulo ![]() . Karena
. Karena ![]() , diperoleh
, diperoleh
![]()
juga merupakan himpunan kelas residu tereduksi lengkap modulo ![]() . Akibatnya diperoleh
. Akibatnya diperoleh
![]()
Karena ![]() , diperoleh
, diperoleh
![]()
[/learn_more]
Contoh:
Tentukan sisa pembagian ![]() oleh 49.
oleh 49.
Solusi:
Perhatikan bahwa ![]() . Berdasarkan Teorema Euler, diperoleh
. Berdasarkan Teorema Euler, diperoleh
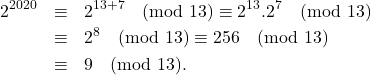
Dengan demikian, sisa pembagiannya adalah ![]() .
.
Contoh:
Diberikan bilangan prima ![]() . Tunjukkan bahwa
. Tunjukkan bahwa ![]() .
.
Solusi:
Diperhatikan bahwa ![]() . Berdasarkan Teorema Kecil Fermat,
. Berdasarkan Teorema Kecil Fermat, ![]() dan
dan ![]() . Karena
. Karena ![]() dan
dan ![]() , maka berdasarkan Teorema Euler diperoleh
, maka berdasarkan Teorema Euler diperoleh ![]() . Jadi,
. Jadi, ![]() untuk
untuk ![]() dan
dan ![]() . Akibatnya
. Akibatnya ![]() .
.
Selanjutnya, Pembaca dapat mengerjakan soal-soal berikut sebagai latihan.
- Tentukan sisa pembagian
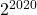 oleh
oleh 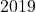 .
. - Tentukan sisa pembagian
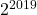 oleh
oleh 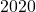 .
. - Tunjukkan bahwa untuk setiap bilangan bulat positif
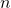 berlaku
berlaku 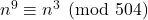 .
. - Diberikan
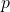 dan
dan 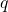 bilangan prima berbeda. Tunjukkan bahwa berlaku
bilangan prima berbeda. Tunjukkan bahwa berlaku
![Rendered by QuickLaTeX.com \[ pq|(20^{pq}-20^p-20^q+20). \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-25162ff7c39aa37aa9f794d71bcf77e7_l3.png)
- Tunjukkan bahwa untuk setiap bilangan genap positif
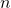 berlaku
berlaku 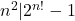 .
. - Tunjukkan bahwa untuk setiap bilangan prima
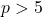 berlaku
berlaku 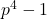 merupakan kelipatan
merupakan kelipatan 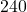 .
.
a. Tentukan jumlah semua bilangan bulat positif yang kurang dari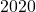 dan relatif prima dengan 2020.
dan relatif prima dengan 2020.
b. Tentukan jumlah semua bilangan bulat positif yang kurang dari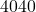 dan relatif prima dengan 2020.
dan relatif prima dengan 2020. - Diberikan
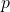 bilangan prima. Tunjukkan bahwa
bilangan prima. Tunjukkan bahwa 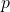 membagi
membagi 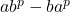 untuk setiap bilangan bulat positif
untuk setiap bilangan bulat positif  dan
dan 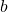 .
.
0 Comments