Kongruensi merupakan cara lain untuk menyajikan keterbagian. Keterbagian merupakan kejadian khusus dari kongrensi ini.
Pada Artikel ini akan dibahas definisi kongruensi dan sifat-sifatnya.
Pengertian dan Definisi Kongruensi
Seperti halnya pada keterbagian, kongruensi berhubungan dengan suatu bilangan bulat tertentu sebut saja ![]() yang nantinya akan disebut dengan modulo
yang nantinya akan disebut dengan modulo ![]() . Notasi dari kongruensi adalah
. Notasi dari kongruensi adalah ![]() dan dibaca kongruen. Sebagai contoh
dan dibaca kongruen. Sebagai contoh ![]() dibaca sebagai
dibaca sebagai ![]() kongruen dengan
kongruen dengan ![]() modulo
modulo ![]() Seringkali untuk menyingkat penulisan, tanda kurung biasanya tidak ditulis. Dalam hal
Seringkali untuk menyingkat penulisan, tanda kurung biasanya tidak ditulis. Dalam hal ![]() tidak kongruen dengan
tidak kongruen dengan ![]() kita tulis dengan
kita tulis dengan ![]() .
.
Definisi 1 (Definisi Modulo)
[box] Diberikan bilangan asli ![]() Untuk sebarang bilangan bulat
Untuk sebarang bilangan bulat ![]() dan
dan ![]() kita punya bahwa
kita punya bahwa ![]() jika dan hanya jika
jika dan hanya jika ![]() Dengan kata lain sesuai dengan definisi keterbagian
Dengan kata lain sesuai dengan definisi keterbagian ![]() jika terdapat bilangan bulat
jika terdapat bilangan bulat ![]() sehingga
sehingga ![]() [/box]
[/box]
Contoh 2
![]() ,
, ![]() ,
, ![]() , dan sebagainya.
, dan sebagainya.
Langsung dari Definisi 1, dapat diturunkan beberapa sifat yang disajikan pada teorema sebagai berikut.
Teorema 3
[box]
Diberikan sebarang bilangan asli ![]() Untuk setiap
Untuk setiap ![]()
berlaku:
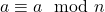
- Jika
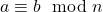 maka
maka 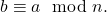
- Jika
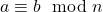 maka
maka 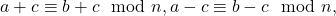 dan
dan 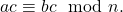
- Jika
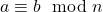 dan
dan 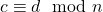 maka
maka 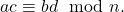 [/box]
[/box]
Bukti hampir sama pada bukti saat kita membahas keterbagian dan diserahkan kepada pembaca sebagai latihan.
Dari sifat 4 pada Teorema 3 diperoleh akibat sebagai berikut.
Akibat 4
[box] Jika ![]() , maka
, maka ![]() , untuk setiap bilangan asli m. [/box]
, untuk setiap bilangan asli m. [/box]
[learn_more caption=”Bukti:” state=”open”]
Kita punya ![]() , maka menurut sifat 4 pada Teorema 3 akan berlaku
, maka menurut sifat 4 pada Teorema 3 akan berlaku ![]() ,
, ![]() , dan
, dan
seterusnya dengan menggunakan induksi matematika dapat diperoleh bahwa ![]() .
.![]()
[/learn_more]
Akibat 4 di atas juga dapat dibuktikan dengan menggunakan Binomial Newton. Salah satu kegunaan dari Akibat ?? adalah untuk mencari satu atau beberapa
digit terakhir dari suatu bilangan asli yang cukup besar.
Contoh 5
Tentukan digit terakhir dari ![]()
Pembahasan:
Digit terakhir dari suatu bilangan bulat adalah sisa pembagian bilangan tersebut oleh 10. Perhatikan bahwa ![]() dengan menggunakan Akibat 4 kita punya bahwa
dengan menggunakan Akibat 4 kita punya bahwa ![]() Dengan demikian, digit terakhir dari
Dengan demikian, digit terakhir dari ![]() adalah
adalah ![]()
Contoh 6
Tentukan dua digit terakhir dari ![]() (Soal OSP 2002).
(Soal OSP 2002).
Pembahasan:
Perhatikan bahwa ![]() Jadi
Jadi ![]() untuk suatu bilangan bulat
untuk suatu bilangan bulat ![]() Sekarang kita punya bahwa
Sekarang kita punya bahwa ![]() Dengan demikian, dua digit terakhir dari
Dengan demikian, dua digit terakhir dari ![]() adalah
adalah ![]()
Selain untuk menentukan digit terakhir dari suatu bilangan asli, kongruensi ini juga dapat digunakan untuk menyelesaikan persamaan baik itu mencari solusi ataupun membuktikan ketidakadaan solusi.
Contoh 7
Tentukan semua solusi asli dari persamaan ![]()
Pembahasan:
Karena ruas kanan genap maka ruas kiripun juga genap, dengan demikian ![]() dan
dan ![]() harus sama paritasnya. Perhatikan bahwa jika
harus sama paritasnya. Perhatikan bahwa jika ![]() maka
maka ![]() dan jika
dan jika ![]() maka
maka ![]() Dengan demikian, jika
Dengan demikian, jika ![]() dan
dan ![]() keduanya ganjil maka
keduanya ganjil maka ![]() yang tentu saja tidak habis dibagi
yang tentu saja tidak habis dibagi ![]() padahal kita tahu bahwa ruas kanan habis dibagi
padahal kita tahu bahwa ruas kanan habis dibagi ![]() Jadi
Jadi ![]() dan
dan ![]() keduanya genap. Misalkan
keduanya genap. Misalkan ![]() dan
dan ![]() untuk suatu bilangan asli
untuk suatu bilangan asli ![]() dan
dan ![]() Kita masukkan ke persamaan awal diperoleh
Kita masukkan ke persamaan awal diperoleh ![]() yang ekivalen dengan
yang ekivalen dengan ![]() Proses ini dapat kita lanjutkan sampai kita dapat
Proses ini dapat kita lanjutkan sampai kita dapat ![]() dan
dan ![]() yang selnjutnya diperoleh
yang selnjutnya diperoleh ![]() Persamaan terakhir ini hanya mempunyai solusi
Persamaan terakhir ini hanya mempunyai solusi ![]() Dengan demikian
Dengan demikian ![]() dan
dan ![]() Jadi satu-satunya solusi adalah
Jadi satu-satunya solusi adalah ![]()
Perhatikan kembali sifat ke tiga pada Teorema 3, yakni jika ![]() maka
maka ![]() untuk setiap bilangan bulat
untuk setiap bilangan bulat ![]() Bagaimana sebaliknya? Jika
Bagaimana sebaliknya? Jika ![]() apakah berakibat
apakah berakibat ![]() Jawabannya tida selalu. Sebagai contoh kita punya
Jawabannya tida selalu. Sebagai contoh kita punya ![]() Akan tetapi, ini tidak berakibat
Akan tetapi, ini tidak berakibat ![]() Lantas, syarat apa yang harus ditambahkan agar berlaku sifat demikian?
Lantas, syarat apa yang harus ditambahkan agar berlaku sifat demikian?
Teorema 8
[box] Diberikan bilangan asli ![]() Jika
Jika ![]() dan
dan ![]() maka
maka ![]() [/box]
[/box]
[learn_more caption=”Bukti:” state=”open”]
Karena ![]() maka
maka ![]() dan karena
dan karena ![]() maka
maka ![]() yang tentu saja berarti
yang tentu saja berarti ![]()
[/learn_more]
0 Comments