Pada himpunan ![]() dapat didefinisikan relasi
dapat didefinisikan relasi ![]() dengan definisi untuk setiap
dengan definisi untuk setiap ![]()
![]()
Berdasarkan relasi ![]() didefinisikan relasi
didefinisikan relasi ![]() dengan definisi untuk setiap
dengan definisi untuk setiap ![]()
![]()
Mudah dibuktikan ![]() jika dan hanya jika
jika dan hanya jika ![]() , sehingga diperoleh
, sehingga diperoleh ![]() jika dan hanya jika dapat ditemukan
jika dan hanya jika dapat ditemukan ![]() yang memenuhi
yang memenuhi ![]()
Teorema 1
Relasi ![]() merupakan relasi urutan parsial tegas dan untuk setiap
merupakan relasi urutan parsial tegas dan untuk setiap ![]() dan
dan ![]() di
di ![]() berlaku tepat satu dari pernyataan-pernyataan
berlaku tepat satu dari pernyataan-pernyataan
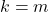
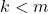
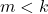 .
.
[learn_more caption=”Bukti:” state=”open”]
- Diambil sebarang
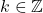 dan diandaikan
dan diandaikan 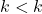 . Akibatnya terdapat
. Akibatnya terdapat 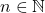 yang memenuhi
yang memenuhi 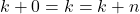 . Sesuai Teorema 3 pada artikel Sistem Bilangan Bulat
. Sesuai Teorema 3 pada artikel Sistem Bilangan Bulat 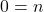 . Kontradiksi dengan
. Kontradiksi dengan 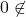 . Akibatnya
. Akibatnya 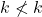 .Untuk sebarang
.Untuk sebarang 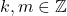 jika
jika 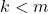 dapat ditemukan
dapat ditemukan 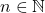 yang memenuhi
yang memenuhi 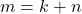 . Jika
. Jika 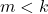 akibatnya terdapat
akibatnya terdapat 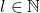 sehingga
sehingga 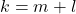 , sehingga
, sehingga
![Rendered by QuickLaTeX.com \[ m = k + n = (m + l) + n = m + (l + n). \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-a60ac3d034b8081a974326dc4683aafe_l3.png)
Sesuai Teorema 3 artikel Sistem Bilangan Bulat
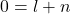 , sedangkan
, sedangkan 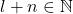 . Kontradiksi. Jadi
. Kontradiksi. Jadi 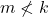 .Selanjutnya untuk sebarang
.Selanjutnya untuk sebarang 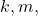 dan
dan 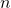 di
di 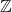 yang memenuhi
yang memenuhi 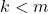 dan
dan  dapat ditemukan
dapat ditemukan 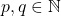 sehingga
sehingga
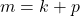 dan
dan 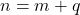 . Akibatnya
. Akibatnya ![Rendered by QuickLaTeX.com \[ n = m + q = (k + p) + q = k + (p + q) \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-e6878468e19599f0a10f3c4dc24c018b_l3.png)
dengan
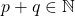 . Dapat disimpulkan
. Dapat disimpulkan 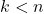 .
. - Diambil sebarang
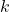 dan
dan 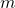 elemen
elemen 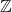 . Dimisalkan
. Dimisalkan 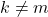 :
:
(a) Jika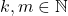 , jelas dapat ditemukan
, jelas dapat ditemukan 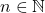 yang memenuhi
yang memenuhi 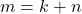 atau
atau 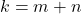
(b) Jika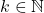 dan
dan 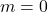 , berlaku
, berlaku 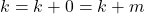 .
.
(c) Jika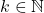 dan
dan 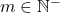 , dapat ditemukan
, dapat ditemukan 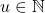 yang memenuhi
yang memenuhi 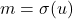 . Diperoleh
. Diperoleh
![Rendered by QuickLaTeX.com \[ k = 0 + k = (\sigma(u) + u) + k = m + (u + k) \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-d13f139e53eda0813d8c4230f6353744_l3.png)
dengan
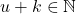 .
.
(d) Jika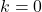 dan
dan 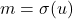 untuk suatu
untuk suatu 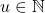 ,
, 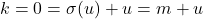 .
.
(e) Jika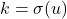 dan
dan 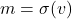 untuk suatu
untuk suatu 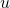 dan
dan  di
di 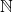 , dari bukti awal
, dari bukti awal
dapat ditentukan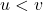 atau
atau 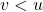 . Jika
. Jika 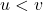 (analog untuk kasus
(analog untuk kasus 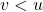 ), dapat ditemukan
), dapat ditemukan 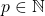 yang memenuhi
yang memenuhi 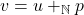 . Akibatnya
. Akibatnya![Rendered by QuickLaTeX.com \[ k = \sigma(u) = \sigma(v -_{\mathbb{N}} p) = \sigma(v) + p \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-7bd3470a1d3bbf561c97216df7e0ae4a_l3.png)

[/learn_more]
Sebagian langkah bukti yang analog tidak dibahas dan ditinggal sebagai latihan.
Teorema 2
Diketahui ![]() dan
dan ![]() bilangan bulat.
bilangan bulat.
- Jika
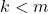 , maka
, maka 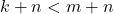 .
. - Jika
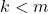 , maka
, maka 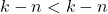 .
. - Diketahui
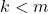 . Jika
. Jika 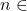 , maka
, maka 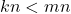 . Jika
. Jika 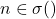 , maka
, maka 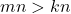 .
.
[learn_more caption=”Bukti:” state=”open”]
Hanya akan dibuktikan untuk 3. Diketahui ![]() . Dapat ditemukan
. Dapat ditemukan ![]() yang memenuhi
yang memenuhi ![]() . Akibatnya
. Akibatnya ![]() . Jika
. Jika ![]() , berlaku
, berlaku ![]() , sehingga terdapat
, sehingga terdapat ![]() yang memenuhi
yang memenuhi ![]() . Jadi
. Jadi ![]() . Jika
. Jika ![]() , maka
, maka ![]() . Akibatnya
. Akibatnya
![]()
dengan ![]() . Karena
. Karena ![]() , maka
, maka ![]() , sehingga
, sehingga ![]() .
. ![]()
[/learn_more]
Seperti yang telah dibahas dalam sistem bilangan asli, setiap bilangan asli ![]() berlaku
berlaku ![]() untuk suatu bilangan asli
untuk suatu bilangan asli ![]() . Hal ini berakibat untuk sebarang bilangan bulat
. Hal ini berakibat untuk sebarang bilangan bulat ![]() ,
, ![]() , sehingga diperoleh sifat berikut ini:
, sehingga diperoleh sifat berikut ini:
Lemma 1
Untuk sebarang bilangan bulat ![]() tidak mungkin terdapat
tidak mungkin terdapat ![]() yang memenuhi
yang memenuhi ![]() .
.
Berbeda dengan sistem bilangan asli, pada sistem bilangan bulat tidak dikenal sifat “Well Ordering set”, yang menyatakan setiap himpunan tak kosong selalu memiliki elemen paling kecil. Namun demikian sistem bilangan bulat masih mempertahankan sifat interval hingga, yaitu untuk setiap ![]() dan
dan ![]() di
di ![]() jika
jika ![]() , maka banyaknya bilangan bulat yang terletak di antara kedua bilangan tersebut hanya sebanyak hingga.
, maka banyaknya bilangan bulat yang terletak di antara kedua bilangan tersebut hanya sebanyak hingga.
Selanjutnya untuk sebarang ![]() ,
, ![]() , dan
, dan ![]() di
di ![]() notasi
notasi ![]() menyatakan
menyatakan ![]() dan
dan ![]() . Demikian juga notasi
. Demikian juga notasi ![]() menyatakan
menyatakan ![]() dan
dan ![]() ; serta notasi-notasi sejenis.
; serta notasi-notasi sejenis.
Definisi 1
Diketahui ![]() dan
dan ![]() didefinisikan himpunan-himpunan sebagai berikut ini:
didefinisikan himpunan-himpunan sebagai berikut ini:
Sebagai gambaran diberikan beberapa contoh berikut ini
![]()
Selain itu mudah ditunjukkan bahwa untuk sebarang ![]() :
:
![Rendered by QuickLaTeX.com [k, m] = \{ k, k + 1, \ldots, m \}](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-df53350466f7562acefeb7344ec85394_l3.png) jika dan hanya jika
jika dan hanya jika 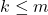 .
.![Rendered by QuickLaTeX.com [k, m) \neq \emptyset \neq (k, m]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-6317d3acc251a7cb76750e5c51c3b0d2_l3.png) jika dan hanya jika
jika dan hanya jika 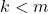 .
.![Rendered by QuickLaTeX.com (k, m] \neq \emptyset](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-f52c629abb562cf55f632b60e5979665_l3.png) jika dan hanya jika
jika dan hanya jika 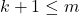 .
.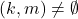 jika dan hanya jika
jika dan hanya jika 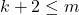 .
.
Sebagai bukti hanya akan ditunjukkan untuk kasus 1 dan 4. Jika ![]() , berarti
, berarti ![]() . Sebaliknya jika
. Sebaliknya jika ![]() , maka
, maka ![]() atau terdapat
atau terdapat ![]() yang memenuhi
yang memenuhi ![]() , dengan
, dengan ![]() . Untuk
. Untuk ![]() diperoleh
diperoleh ![]() . Untuk
. Untuk ![]() ,
,
![]()
Jadi ![]()
Untuk kasus ![]() . Jika
. Jika ![]() , diperoleh untuk sebarang
, diperoleh untuk sebarang ![]() yang memenuhi
yang memenuhi ![]() akan berakibat
akan berakibat
![]()
maka terdapat ![]() yang memenuhi
yang memenuhi ![]() . Akibatnya
. Akibatnya ![]() , sehingga
, sehingga ![]() . Kontradiksi dengan Lemma 1. Dapat disimpilkan
. Kontradiksi dengan Lemma 1. Dapat disimpilkan ![]() . Sebaliknya jika
. Sebaliknya jika ![]() , berlaku
, berlaku ![]() .
.
0 Comments