Seiring dengan perkembangan budaya masyarakat baik dalam ilmu pengetahuan, kehidupan sehari-hari maupun dalam ekonomi sistem bilangan asli yang telah berkembang dianggap masih belum mampu mencukupi fenomena dunia matematika serta kebutuhan masyarakat tentang alat hitung. Khususnya bilangan yang bisa mewakili “ketiadaan unsur” dalam suatu himpunan serta konsep “kekurangan” sebanyak tertentu dari suatu kondisi. Sebagai contoh Aladin memiliki 3 ekor kambing. Untuk menjamu ayah Yasmin dan rombongan keluarga Aladin akan memotong kambing. Tentu saja jika 3 kambing tersebut disembelih 2, masalah banyaknya kambing Aladin yang tersisa dapat dirumuskan secara matematis, yaitu
![]()
Namun jika 3 ekor kambing itu dipotong semua, masalah tidak bisa dirumuskan secara matematis menggunakan sistem bilangan asli dalam artikel sebelumnya (Sistem Bilangan Asli ) dengan
![]()
karena tidak ada bilangan asli yang bisa mengisi ![]() .
.
Demikian juga pada masalah berikut ini. Misalkan ternyata rombongan tersebut sangat besar, sehingga dibutuhkan 4 kambing untuk dipotong. Padahal di kandang Aladin hanya tersedia 3 kambing. Terdapat “kekurangan” 1 ekor kambing yang tidak bisa dijelaskan menggunakan sistem bilangan asli yang sudah dikembangkan. Untuk mencukupinya Aladin harus “meminjam” 1 kambing tetangganya.
Artikel ini sangat bermanfaat untuk pembaca untuk mengenal salah satu dasar matematika yaitu bilangan bulat dan ladasan pengkonstruksiannya.
Selanjutnya, solusi dari persamaan ![]() untuk
untuk ![]() yang diberikan, belum tentu bisa diperoleh di
yang diberikan, belum tentu bisa diperoleh di ![]() . Solusi
. Solusi ![]() , hanya bisa
, hanya bisa
diperoleh untuk ![]() . Untuk persamaan
. Untuk persamaan ![]() , solusi
, solusi ![]() bukan elemen
bukan elemen ![]() . Untuk itu diperlukan himpunan
. Untuk itu diperlukan himpunan ![]() yang merupakan perluasan
yang merupakan perluasan ![]() , sehingga persamaan tersebut selalu bisa ditemukan solusinya.
, sehingga persamaan tersebut selalu bisa ditemukan solusinya.
Untuk itu perlu dikonstruksi sistem bilangan baru yang memuat sistem bilangan asli sebagai subbagiannya dengan operasi-operasi yang berlaku pada sistem yang baru merupakan perluasan dari operasi-operasi pada ![]() .
.
Definisi 1
Diketahui ![]() himpunan semua bilangan asli. Diambil
himpunan semua bilangan asli. Diambil ![]() sebarang himpunan yang berbeda semua elementnya sehingga
sebarang himpunan yang berbeda semua elementnya sehingga
![]()
pemetaan bijektif. Jadi ![]() . Selanjutnya diambil
. Selanjutnya diambil ![]() .
.
Himpunan ![]() yang dilengkapi dengan operasi biner “
yang dilengkapi dengan operasi biner “![]() ” dan “
” dan “![]() ” yang meemenuhi:
” yang meemenuhi:
- Untuk semua
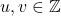 , didefinisikan
, didefinisikan 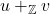 salah satu dari; untuk masing-masing
salah satu dari; untuk masing-masing 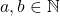 :
:
1.1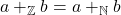
1.2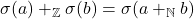
1.3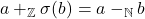 , jika
, jika 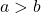 ,
,
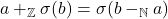 , jika
, jika 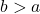 ,
,
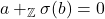 , jika
, jika 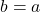
1.4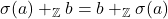
1.5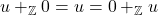
- Untuk semua
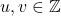 , didefinisikan
, didefinisikan 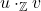 salah satu dari; untuk masing-masing
salah satu dari; untuk masing-masing 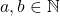 :
:
2.1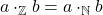
2.2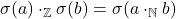
2.3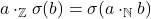
2.4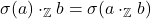
2.5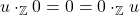
Untuk mempermudah penulisan pada artikel ini yang ditulis dengan ![]() dan
dan ![]() adalah
adalah ![]() dan
dan ![]() . Dari definisi tersebut terlihat dengan jelas, bahwa
. Dari definisi tersebut terlihat dengan jelas, bahwa ![]() dan operasi
dan operasi ![]() merupakan perluasan dari
merupakan perluasan dari ![]() ; sedangkan
; sedangkan ![]() merupakan perluasan dari
merupakan perluasan dari ![]() .
.
Berdasarkan definisi operasi penjumlahan dan perkalian pada ![]() dapat dibuktikan bahwa kedua operasi tersebut bersifat asosiatif.
dapat dibuktikan bahwa kedua operasi tersebut bersifat asosiatif.
Teorema 1
Untuk setiap ![]() berlaku:
berlaku:
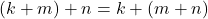 , dan
, dan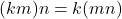 .
.
[learn_more caption=”Bukti:” state=”open”]
- Diambil sebarang
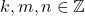 akan dibuktikan assosiatif terhadap
akan dibuktikan assosiatif terhadap 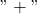 .(a) Jika
.(a) Jika 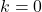 atau
atau 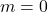 atau
atau 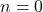
Jika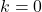 ,
, 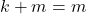 dan
dan 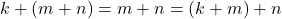
Jika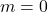 ,
, 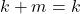 dan
dan 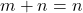 , sehingga
, sehingga 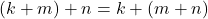
Jika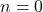 ,
, 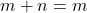 dan
dan 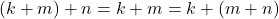
(b) Jika
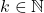 :
:
i. Jika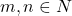 ,
, 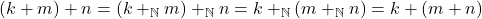
ii. Jika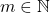 ,
, 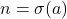 untuk suatu
untuk suatu 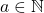 berlaku
berlaku 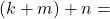
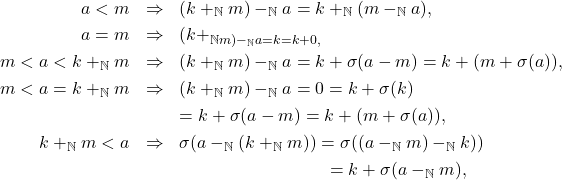
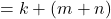 .
.iii. Jika
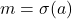 untuk suatu
untuk suatu 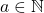 , berlaku
, berlaku 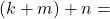
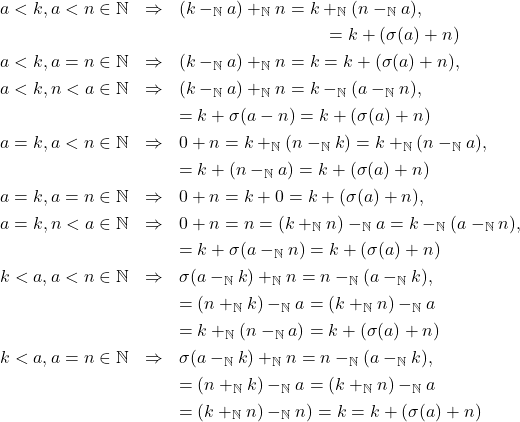
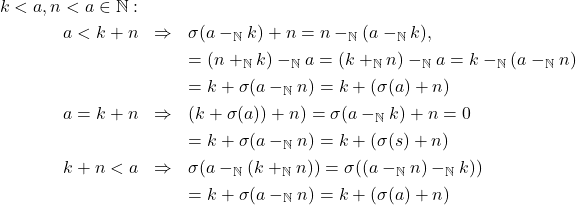
iv. Jika
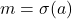 dan
dan 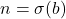 untuk suatu
untuk suatu 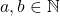 , berlaku
, berlaku 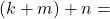
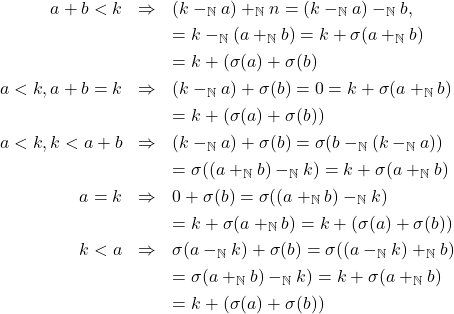
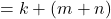 .
.(c) Jika
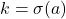 untuk suatu
untuk suatu 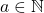
i.
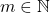 dan
dan 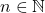 ,
, 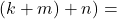
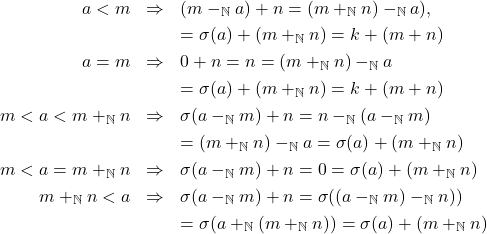
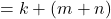 .
.ii.
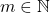 dan
dan 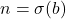 untuk suatu
untuk suatu 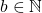 ,
, 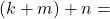
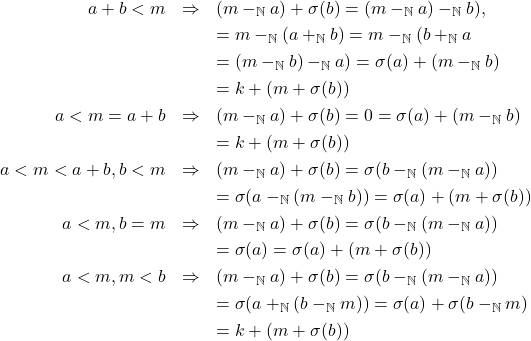
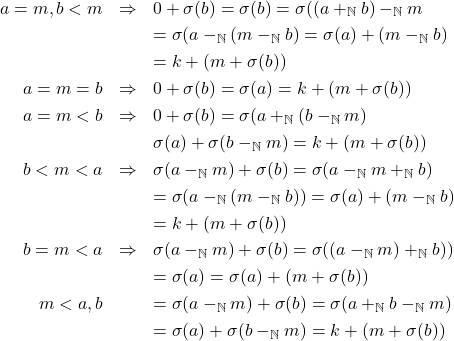
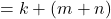 .
.iii. Terdapat
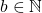 sehingga
sehingga 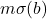 dan
dan 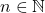 ,
, 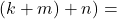
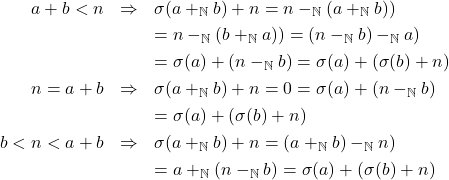
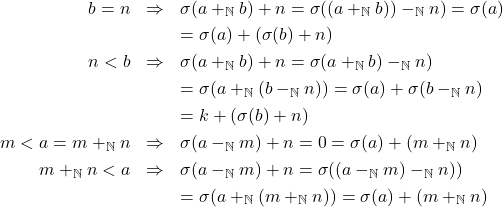
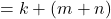 .
.iv. Terdapat
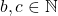 yang memenuhi
yang memenuhi 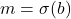 dan
dan 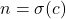 ,
,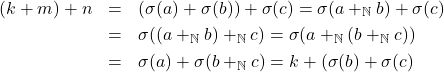
- Untuk
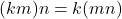 hanya akan dibuktikan sebagian. Bagian yang belum dibuktikan diberikan untuk latihan. Diambil sebarang
hanya akan dibuktikan sebagian. Bagian yang belum dibuktikan diberikan untuk latihan. Diambil sebarang 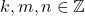 .
.
(a) Jika
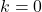 atau
atau 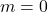 atau
atau 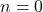 berlaku
berlaku![Rendered by QuickLaTeX.com \[ (km)n = 0n = 0 = 0(mn) = k(mn) \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-bb0b07513f57fc1b296889eac8337ee4_l3.png)
Kasus
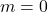 atau
atau 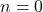 analog.
analog.(b) Jika
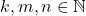
![Rendered by QuickLaTeX.com \[ (km)n = (k\cdot_{\mathbb{N}}m)\cdot_{\mathbb{N}} n = k\cdot_{\mathbb{N}}(m \cdot_{\mathbb{N}} n) = k(mn). \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-10cdea6edaffd9cafdfb398ba2ea2e15_l3.png)
(c) Jika
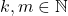 dan
dan 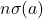 untuk suatu
untuk suatu 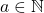
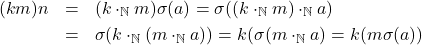
(d) Jika
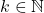 ,
, 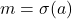 , dan
, dan 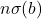 untuk suatu
untuk suatu 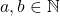
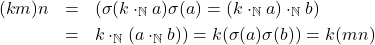
(e) Jika
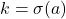 ,
, 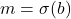 , dan
, dan 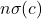 untuk suatu
untuk suatu 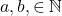
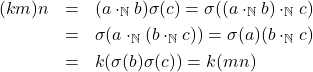
[/learn_more]
Teorema 2
Pada himpunan ![]() berlaku sifat.
berlaku sifat.
- Untuk setiap
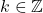 terdapat dengan
terdapat dengan 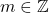 ,
, 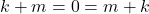
- Komutatif : untuk setiap
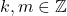 ,
, 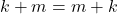 dan
dan 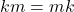 .
. - Distributif : untuk setiap
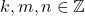
![Rendered by QuickLaTeX.com \[ k(m + n) = km + kn~~{\rm dan}~~(k + m)n = kn + mn \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-eb9e970c3ddd658524b8dbe6ea9ee57c_l3.png)
- Untuk setiap
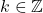 ,
, 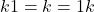 .
.
[learn_more caption=”Bukti:” state=”open”]
- Misalkan
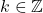 . Jika
. Jika 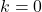 dipilih
dipilih 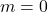 . Jika
. Jika 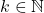 , diambil
, diambil 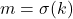 . Untuk
. Untuk 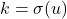 untuk suatu
untuk suatu 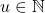 diambil
diambil  sehingga berlaku
sehingga berlaku 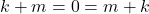 .
. - Langsung dari Aksioma 1 dan 2.
- Karena komutatif berlaku, sifat distributif cukup dibuktikan satu sisi. Diambil sebarang
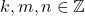 . Hanya akan dibuktikan untuk kasus
. Hanya akan dibuktikan untuk kasus 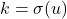 ,
, 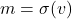 , dengan
, dengan 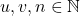 . Kasus yang lain ditinggal untuk latihan.
. Kasus yang lain ditinggal untuk latihan.
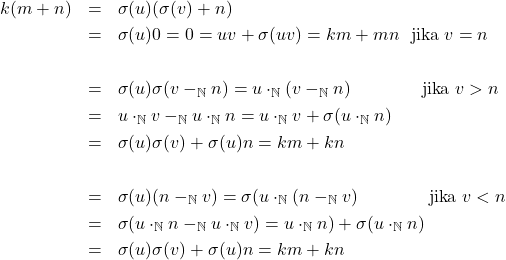
- Jika
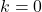 atau
atau 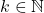 , sifat jelas berlaku. Jika
, sifat jelas berlaku. Jika 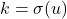 untuk suatu
untuk suatu 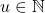 berlaku
berlaku
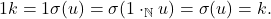
 .
.
[/learn_more]
Teorema 3
Untuk setiap ![]() :
:
- Jika
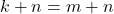 , maka
, maka 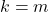
- Jika
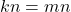 dan
dan 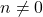 , maka
, maka 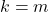
- Jika
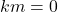 , maka
, maka 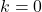 atau
atau 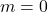 .
.
[learn_more caption=”Bukti:” state=”open”]
Diambil sebarang ![]()
- Jika
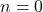 , jelas
, jelas 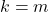 . Jika
. Jika 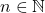 , maka
, maka
![Rendered by QuickLaTeX.com \[ k = k + (n + \sigma(n)) = (k + n) + \sigma(n) = (m + n) + \sigma(n) = m + (n + \sigma(n)) = m \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-2c56c345a95c2902d99d08d91474e285_l3.png)
Untuk
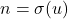 untuk suatu
untuk suatu 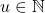 , maka
, maka![Rendered by QuickLaTeX.com \[ k = k + (\sigma(u) + u) = (k + n) + u = (m + n) + u = m + (\sigma(u) + u) = m \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-d4ef7e2b8403fadb287790f0a4d0506e_l3.png)
- Untuk
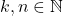 berlaku
berlaku 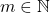 . Akibatnya sesuai sifat-sifat
. Akibatnya sesuai sifat-sifat 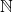 ,
, 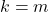 . Untuk
. Untuk 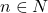 dan
dan 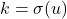 untuk suatu
untuk suatu 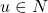 . Jelas
. Jelas 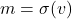 untuk suatu
untuk suatu 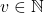 , sehingga
, sehingga
![Rendered by QuickLaTeX.com \[ \sigma(u\cdot_{\mathbb{N}}n) = \sigma(u)n = \sigma(v)n = \sigma(v\cdot_{\mathbb{N}}n) \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-944a233175f2e88349a355c2cdb19055_l3.png)
Dapat disimpulkan
 , sehingga
, sehingga  dan
dan 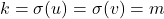 .
.
Untuk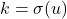 ,
, 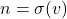 untuk suatu
untuk suatu 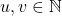 . Akibatnya
. Akibatnya 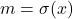 untuk suatu
untuk suatu 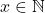 .
.![Rendered by QuickLaTeX.com \[ \sigma(u\cdot{\mathbb{N}}v) = \sigma(u)\sigma(v) = \sigma(x)\sigma(v) = \sigma(x\cdot_{\mathbb{N}}v) \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-57f3e4e7d7cff472b24fa506c6eddd46_l3.png)
sehingga
 . sesuai sifat bilangan asli
. sesuai sifat bilangan asli  .
. - Diketahui
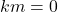 . Andaikan
. Andaikan 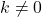 dan
dan 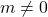 . Sesuai sifat 2
. Sesuai sifat 2 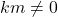 . Kontradiksi.
. Kontradiksi. 
[/learn_more]
Akibat langsung dari Teorema 3 eksistensi ![]() pada Teorema 1 tunggal, yaitu untuk setiap
pada Teorema 1 tunggal, yaitu untuk setiap ![]() terdapat dengan tunggal
terdapat dengan tunggal ![]() yang memenuhi
yang memenuhi ![]() . Elemen
. Elemen ![]() didefinisikan sebagai invers
didefinisikan sebagai invers ![]() terhadap penjumlahan yang ditulis
terhadap penjumlahan yang ditulis ![]() . Selanjutnya dapat didefinisikan operasi pengurangan
. Selanjutnya dapat didefinisikan operasi pengurangan ![]() dengan
dengan
![]()
untuk setiap ![]() .
.
Teorema 4
Untuk setiap ![]() :
:
- Jika
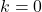 , maka
, maka 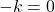
- Jika
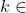 , maka
, maka 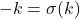 .
. - Jika
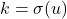 untuk suatu
untuk suatu 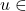 , maka
, maka 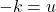 .
.
[learn_more caption=”Bukti:” state=”open”]
Diketahui ![]() .
.
- Karena
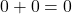 , maka
, maka 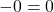
- Jika
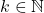 ,
, 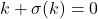 , sehingga
, sehingga 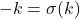 .
. - Karena
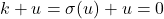 , maka
, maka 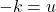
 .
.
[/learn_more]
Dari teorema tersebut untuk sebarang ![]() dapat diberikan notasi baru yaitu
dapat diberikan notasi baru yaitu ![]() sehingga
sehingga
![]()
sedangkan ![]() untuk sebarang
untuk sebarang ![]() . Akibatnya jika
. Akibatnya jika ![]() memenuhi
memenuhi
![]()
sehingga ![]() .
.
Teorema 5
Diketahui ![]() ,
, ![]() , dan
, dan ![]() elemen-elemen
elemen-elemen ![]() .
.
[learn_more caption=”Bukti:” state=”open”]
Diketahui ![]() :
:
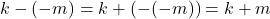
- Dipenuhi
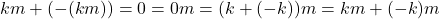 . Sesuai Teorema 3 disimpulkan
. Sesuai Teorema 3 disimpulkan 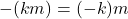 . Secara analog dapat dibuktikan
. Secara analog dapat dibuktikan 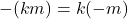 .
. 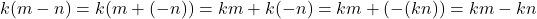 .
.  .
.
[/learn_more]
Selanjutnya berdasarkan Definisi 1 di atas dapat dipastikan bahwa ![]() merupakan perluasan dari sistem bilangan asli
merupakan perluasan dari sistem bilangan asli ![]() .
.
0 Comments