Seperti yang telah dikenal baik pada materi dasar logika relasi ![]() pada himpunan yang tidak kosong
pada himpunan yang tidak kosong ![]() disebut relasi urutan (parsial) jika refleksif, antisimetris, dan transitif. Relasi
disebut relasi urutan (parsial) jika refleksif, antisimetris, dan transitif. Relasi ![]() disebut relasi urutan tegas jika irrefleksif, asimetris, dan transitif. Himpunan
disebut relasi urutan tegas jika irrefleksif, asimetris, dan transitif. Himpunan ![]() yang dilengkapi urutan parsial
yang dilengkapi urutan parsial ![]() disebut himpunan terurut parsial dan setiap elemen
disebut himpunan terurut parsial dan setiap elemen ![]() dan
dan ![]() di
di ![]() yang memenuhi
yang memenuhi ![]() anggota
anggota ![]() biasa ditulis dengan
biasa ditulis dengan ![]() . Jika
. Jika ![]() anggota
anggota ![]() dengan
dengan ![]() relasi urutan tegas ditulis dengan
relasi urutan tegas ditulis dengan ![]() .
.
Pada sistem bilangan asli ![]() dapat dikonstruksi relasi urutan dengan menggunakan sifat-sifat operasi “
dapat dikonstruksi relasi urutan dengan menggunakan sifat-sifat operasi “![]() “. Untuk itu perlu dikaji terlebih dulu sifat elementer berikut ini.
“. Untuk itu perlu dikaji terlebih dulu sifat elementer berikut ini.
Teorema 1
Untuk masing-masing ![]() , dapat ditemukan
, dapat ditemukan ![]() yang memenuhi
yang memenuhi ![]() .
.
[learn_more caption=”Bukti:” state=”open”]
Dibentuk ![]() . Jelas
. Jelas ![]() . Dimisalkan
. Dimisalkan ![]() , berarti
, berarti ![]() atau
atau
![]() untuk suatu
untuk suatu ![]() .
.
Jika ![]() , maka
, maka ![]() . Akibatnya
. Akibatnya ![]() , karena terdapat
, karena terdapat ![]() sehingga
sehingga ![]() . Jika
. Jika ![]() untuk suatu
untuk suatu ![]() ,
,
maka
![]()
Jelas ![]() , akibatnya
, akibatnya ![]() . Sesuai A4 (Definisi Sistem Bilangan Asli), maka
. Sesuai A4 (Definisi Sistem Bilangan Asli), maka ![]() .
. ![]() .
.
[/learn_more]
Teorema 2
Untuk setiap ![]() , berlaku tepat satu pernyataan:
, berlaku tepat satu pernyataan:
[learn_more caption=”Bukti:” state=”open”]
Hanya akan dibuktikan untuk eksistensi ketiga pernyataan. Ketunggalan pernyataan yang berlaku dijadikan latihan. Diambil sebarang ![]() . Dibentuk
. Dibentuk
![]()
Jika ![]() , jelas
, jelas ![]() . Jika
. Jika ![]() , menurut Teorema 1 dapat ditemukan
, menurut Teorema 1 dapat ditemukan ![]() yang memenuhi
yang memenuhi ![]() . Akibatnya
. Akibatnya ![]() . Selanjutnya misalkan
. Selanjutnya misalkan ![]() . Jika
. Jika ![]() , maka
, maka ![]() . Terdapat
. Terdapat ![]() yang memenuhi
yang memenuhi ![]() . Jadi
. Jadi ![]() .
.
Jika dapat ditemukan ![]() yang memenuhi
yang memenuhi ![]() , maka
, maka
![]()
dengan ![]() . Jadi
. Jadi ![]() . Hal ini juga berlaku jika terdapat
. Hal ini juga berlaku jika terdapat ![]() yang memenuhi
yang memenuhi ![]() . Untuk
. Untuk ![]() berakibat
berakibat ![]() yang memenuhi pernyataan pertama. Jadi
yang memenuhi pernyataan pertama. Jadi ![]() . Jika
. Jika ![]() menurut Teorema 1 terdapat
menurut Teorema 1 terdapat ![]() yang memenuhi
yang memenuhi ![]() . Akibatnya
. Akibatnya
![]()
sehingga ![]() .
. ![]()
[/learn_more]
Berdasarkan Teorema 2 dapat diturunkan relasi pada ![]() .
.
Definisi 1
Untuk setiap ![]() didefinisikan
didefinisikan
![]()
Selanjutnya didefinisikan ![]() jika dan hanya jika
jika dan hanya jika ![]() . Relasi
. Relasi ![]() menyatakan
menyatakan ![]() atau
atau ![]() yang merupakan relasi urutan parsial lemah.
yang merupakan relasi urutan parsial lemah.
Contoh 1
![]()
Dari Definisi 1 dapat dinyatakan sifat berikut ini:
Teorema 3
Untuk setiap ![]() berlaku tepat hanya satu
berlaku tepat hanya satu
![]()
Relasi “<” pada Definisi 1 merupakan relasi urutan tegas, seperti yang dinyatakan dalam teorema berikut ini.
Teorema 4
Untuk setiap ![]() berlaku
berlaku
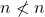
- Jika
 , maka
, maka 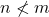
- Jika
 dan
dan 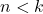 , maka
, maka 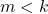
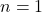 atau
atau 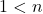
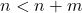
- Jika
 , maka
, maka 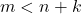
- Jika
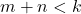 , maka
, maka 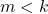
[learn_more caption=”Bukti:” state=”open”]
Hanya dibuktikan untuk pernyataan 3. Diketahui ![]() dan
dan ![]() . Maka dapat ditemukan
. Maka dapat ditemukan ![]() , sehingga
, sehingga
![]()
sehingga ![]() , dengan
, dengan ![]() . Akibatnya
. Akibatnya ![]() .
. ![]()
[/learn_more]
Teorema 5
Untuk setiap ![]() berlaku
berlaku
- Jika
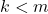 , maka
, maka 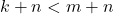
- Jika
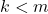 , maka
, maka 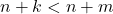
- Jika
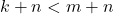 , maka
, maka 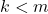
- Jika
 , maka
, maka 
[learn_more caption=”Bukti:” state=”open”]
Hanya akan dibuktikan untuk 1 dan 3.
1. Karena ![]() , maka dapat ditemukan
, maka dapat ditemukan ![]() sehingga
sehingga ![]() . Akibatnya
. Akibatnya
![]()
Dengan kata lain ![]() .
.
3. Terdapat ![]() yang memenuhi
yang memenuhi ![]() . Akibatnya
. Akibatnya ![]() . Menurut kanselasi penjumlahan berlaku
. Menurut kanselasi penjumlahan berlaku ![]() , sehingga
, sehingga ![]() .
. ![]()
[/learn_more]
Selanjutnya, dengan memanfaatkan relasi “![]() ” dapat didefinisikan operasi pengurangan antara dua bilangan asli yang berbeda. Meskipun operasi ini tidak berlaku untuk semua pasangan bilangan asli, namun fenomena yang muncul dari operasi tersebut sangat berperan dalam sistem yang lebih luas.
” dapat didefinisikan operasi pengurangan antara dua bilangan asli yang berbeda. Meskipun operasi ini tidak berlaku untuk semua pasangan bilangan asli, namun fenomena yang muncul dari operasi tersebut sangat berperan dalam sistem yang lebih luas.
Definisi 2
Untuk setiap ![]() di
di ![]() terdapat dengan tunggal
terdapat dengan tunggal ![]() yang memenuhi
yang memenuhi ![]() . Elemen tunggal yang memenuhi kondisi tersebut ditulis dengan
. Elemen tunggal yang memenuhi kondisi tersebut ditulis dengan ![]() .
.
Pada definisi ini terlihat jelas pengurangan ![]() oleh
oleh ![]() dimungkinkan karena adanya syarat cukup
dimungkinkan karena adanya syarat cukup ![]() ; dan bukan karena operasi pengurangan untuk sebarang dua bilangan di
; dan bukan karena operasi pengurangan untuk sebarang dua bilangan di ![]() .
.
Contoh 2
Karena ![]() , dan
, dan ![]() , maka sesuai definisi
, maka sesuai definisi ![]() . Sebaliknya karena
. Sebaliknya karena ![]() , maka tidak dapat didefinisikan
, maka tidak dapat didefinisikan ![]() di
di ![]() .
.
Teorema 6
Untuk setiap ![]() ,
,
- Jika
 , maka
, maka 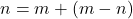
- Jika
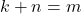 , maka
, maka 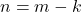
- Jika
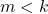 dan
dan 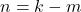 , maka
, maka 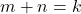
- Jika
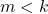 , maka untuk setiap
, maka untuk setiap 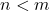 berlaku
berlaku 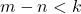
[learn_more caption=”Bukti:” state=”open”]
Hanya untuk 2 dan 4. Untuk 1 dan 3 digunakan untuk latihan.
2 .Karena ![]() , berarti
, berarti ![]() . Menggunakan sifat 1, diperoleh
. Menggunakan sifat 1, diperoleh ![]() . Namun karena bilangan
. Namun karena bilangan ![]() yang memenuhi
yang memenuhi ![]() tunggal, maka
tunggal, maka ![]() .
.
4. Terdapat ![]() yang memenuhi
yang memenuhi ![]() dan
dan ![]() . Akibatnya
. Akibatnya ![]() dan
dan ![]() . Karena
. Karena ![]() , berakibat
, berakibat ![]() .
.![]()
[/learn_more]
Hubungan antara operasi ![]() terhadap pengurangan di antara elemen-elemen
terhadap pengurangan di antara elemen-elemen ![]() mengungkapkan sifat-sifat sistem bilangan asli. Pada teorema berikut ini dipaparkan sebagian di antaranya.
mengungkapkan sifat-sifat sistem bilangan asli. Pada teorema berikut ini dipaparkan sebagian di antaranya.
Teorema 7
Untuk sebarang ![]() berlaku:
berlaku:
- Jika
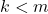 , maka
, maka 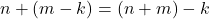
- Jika
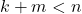 , maka
, maka 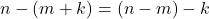
- Jika
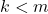 dan
dan  , maka
, maka 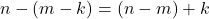
[learn_more caption=”Bukti:” state=”open”]
- Karena
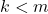 terdapat
terdapat 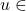 sehingga
sehingga 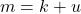 . Jadi
. Jadi 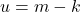 dan
dan 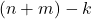 terdefinisi.
terdefinisi.
![Rendered by QuickLaTeX.com \[ n + m = n + (u + k) = (n + u) + k = (n + (m - k)) + k \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-6db7e520cee0395457896cce54e9871e_l3.png)
sehingga
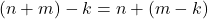 ..
.. - Karena
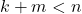 , dapat ditemukan
, dapat ditemukan 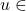 sehingga
sehingga
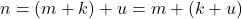 . Berarti
. Berarti 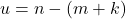 . Sesuai definisi
. Sesuai definisi 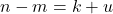 dan
dan  .
.
Terbukti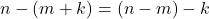
- Diperoleh
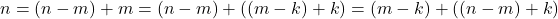 . Akibatnya
. Akibatnya 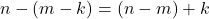 .
. 
[/learn_more]
Selanjutnya salah satu sifat yang berlaku pada sistem bilangan asli dinyatakan dalam teorema berikut ini.
Teorema 8
Pada ![]() tidak mungkin ditemukan barisan tak hingga
tidak mungkin ditemukan barisan tak hingga
![]()
[learn_more caption=”Bukti:” state=”open”]
Andaikan ![]() barisan bilangan-bilangan asli yang memenuhi
barisan bilangan-bilangan asli yang memenuhi ![]() untuk setiap
untuk setiap ![]() . Akibatnya terdapat
. Akibatnya terdapat ![]() yang memenuhi
yang memenuhi
![]()
Namun kemungkinan paling banyak (bisa lebih sedikit) hanya ada barisan
![]()
Kontradiksi.![]()
[/learn_more]
Teorema 9
Di antara dua bilangan asli yang berbeda hanya terdapat sebanyak hingga bilangan asli yang terletak di antara keduanya.
![]()
[learn_more caption=”Bukti:” state=”open”]
Misalkan ![]() . Karena
. Karena ![]() , dapat ditemukan
, dapat ditemukan ![]() sehingga
sehingga ![]() . Jika
. Jika ![]() ,
, ![]() . Jika
. Jika ![]() ,
, ![]() . Jika
. Jika ![]() , diperoleh
, diperoleh
![]()
sehingga ![]() hingga.
hingga. ![]()
[/learn_more]
Akibat dari Teorema 8 dan 9 diperoleh sifat berikut ini.
Sifat 1
Untuk sebarang ![]() yang tidak kosong, selalu ditemukan bilangan terkecil, yaitu bilangan
yang tidak kosong, selalu ditemukan bilangan terkecil, yaitu bilangan ![]() yang memenuhi
yang memenuhi ![]() untuk setiap
untuk setiap ![]() .
.
[learn_more caption=”Bukti:” state=”open”]
Diambil sebarang ![]() . Akibatnya untuk sebarang
. Akibatnya untuk sebarang ![]() berlaku
berlaku ![]() atau
atau ![]() atau
atau ![]() . Jika
. Jika ![]() untuk setiap
untuk setiap ![]() berarti
berarti ![]() merupakan bilangan terkecil sebagai
merupakan bilangan terkecil sebagai ![]() yang dicari. Jika tidak berarti dapat ditemukan
yang dicari. Jika tidak berarti dapat ditemukan ![]() yang memenuhi
yang memenuhi ![]() . Dibentuk
. Dibentuk
![]()
Jelas bahwa ![]() . Menurut Teorema 9
. Menurut Teorema 9 ![]() hingga, sehingga
hingga, sehingga ![]() hingga. Jadi dapat ditemukan
hingga. Jadi dapat ditemukan ![]() yang memenuhi
yang memenuhi ![]() . Kondisi ini berakibat
. Kondisi ini berakibat ![]() dapat diurutkan dan tanpa mengurangi keumuman
dapat diurutkan dan tanpa mengurangi keumuman
![]()
sehingga ![]() merupakan bilangan yang terkecil di
merupakan bilangan yang terkecil di ![]() .
. ![]()
[/learn_more]
0 Comments