Salah satu materi yang diujikan pada Olimpiade Sains Nasional (OSN) [sekarang dikenal dengan nama Kompetisi Sains Nasional] teori bilangan. Pada OSN tahun 2008 yang diselenggarakan di Makasar pada tanggal 8-14 Agustus, soal materi teori bilangan yang diujikan berhubungan dengan keterbagian. Pada artilkel ini, diberikan soal dan pembahasan soal OSN 2008 hari kedua soal teori bilangan.
Soal
Misalkan ![]() bilangan-bilangan bulat sedemikian sehingga
bilangan-bilangan bulat sedemikian sehingga ![]() membagi
membagi ![]() dan
dan ![]() membagi
membagi ![]() .
.
Haruskah ![]() ? Jelaskan.
? Jelaskan.
OSN 2008 Hari Kedua Soal Teori Bilangan
Pembahasan
Diketahui ![]() bilangan-bilangan bulat dan memenuhi
bilangan-bilangan bulat dan memenuhi
![]()
Apakah harus ![]() ?
?
Claim: ![]() .
.
Diperhatikan bahwa
![]()
artinya terdapat bilangan asli ![]() sehingga
sehingga ![]()
Akan dibuktikan bahwa ![]() .
.
Diperhatikan bahwa
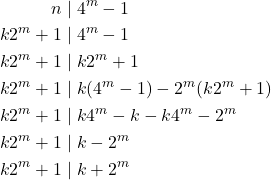
Diperoleh
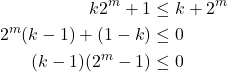
Karena ![]() , maka
, maka ![]() . Jadi haruslah
. Jadi haruslah ![]() , atau dengan kata lain
, atau dengan kata lain ![]() . Karena
. Karena ![]() , diperoleh
, diperoleh ![]() . Jadi haruslah
. Jadi haruslah ![]() .
.

0 Comments