Persamaan Diophantine non-linear adalah suatu persamaan Diophantine yang tidak linear atau dengan kata lain memiliki suku yang berderajat lebih dari 1. Secara umum, tidak ada teknik khusus yang dapat digunakan untuk mencari penyelesaian persamaan Diophantine non-linear. Pada artikel ini, akan dijelaskan beberapa persamaan Diophantine non-linear yang cukup terkenal dan telah diketahui penyelesaiannya, yakni Persamaan Phytagoras, Persamaan Pell,
Persamaan Phytagoras
Persamaan Phytagoras merupakan suatu persamaan Diophantine yang memiliki bentuk
(1) ![]()
Solusi bulat positif ![]() dari persamaan 1 biasanya dikenal dengan istilah tripel Phytagoras. Dari sudut pandang geometri, setiap tripel Phytagoras
dari persamaan 1 biasanya dikenal dengan istilah tripel Phytagoras. Dari sudut pandang geometri, setiap tripel Phytagoras ![]() terkait dengan sebuah segitiga siku-siku yang sisi-sisinya
terkait dengan sebuah segitiga siku-siku yang sisi-sisinya ![]() ,
, ![]() , dan
, dan ![]() . Beberapa tripel Phytagoras yang umum diketahui adalah
. Beberapa tripel Phytagoras yang umum diketahui adalah ![]() ,
, ![]() ,
, ![]() .
.
Suatu tripel Phytagoras ![]() dikatakan primitif jika
dikatakan primitif jika ![]() . Setiap tripel Phytagoras merupakan tripel Phytagoras primitif atau kelipatan suatu tripel Phytagoras primitif. Teorema berikut memberikan formula umum dari tripel Phytagoras primitif.
. Setiap tripel Phytagoras merupakan tripel Phytagoras primitif atau kelipatan suatu tripel Phytagoras primitif. Teorema berikut memberikan formula umum dari tripel Phytagoras primitif.
Teorema 1
[box] Tripel bilangan bulat positif ![]() merupakan tripel Phytagoras primitif jika dan hanya jika
merupakan tripel Phytagoras primitif jika dan hanya jika ![]() memiliki bentuk
memiliki bentuk ![]() atau
atau ![]() di mana
di mana ![]() dan
dan ![]() merupakan bilangan bulat positif yang relatif prima,
merupakan bilangan bulat positif yang relatif prima, ![]() , dan memiliki paritas berbeda.[/box]
, dan memiliki paritas berbeda.[/box]
[learn_more caption=”Bukti:” state=”open”]
Misalkan ![]() adalah tripel Phytagoras primitif. Jika
adalah tripel Phytagoras primitif. Jika ![]() dan
dan ![]() merupakan bilangan ganjil, diperoleh
merupakan bilangan ganjil, diperoleh
![]()
yang merupakan sebuah kontradiksi sebab bilangan kuadrat tidak ekuivalen dengan 2 dalam modulo 4. Akibatnya, salah satu dari ![]() atau
atau ![]() merupakan bilangan genap. Misalkan
merupakan bilangan genap. Misalkan ![]() genap, maka
genap, maka ![]() haruslah ganjil sebab
haruslah ganjil sebab ![]() dan
dan ![]() relatif prima. Akibatnya,
relatif prima. Akibatnya, ![]() juga bilangan ganjil. Diperoleh
juga bilangan ganjil. Diperoleh ![]() dan
dan ![]() adalah bilangan bulat positif. Lebih lanjut,
adalah bilangan bulat positif. Lebih lanjut, ![]() dan
dan ![]() saling relatif prima, sebab setiap faktor persekutuan dari
saling relatif prima, sebab setiap faktor persekutuan dari ![]() dan
dan ![]() akan habis membagi
akan habis membagi ![]() dan
dan ![]() . Karena
. Karena ![]() and
and ![]() , diperoleh
, diperoleh
![]()
Perhatikan bahwa karena ![]() merupakan bilangan bulat dan
merupakan bilangan bulat dan ![]() dan
dan ![]() saling relatif prima, diperoleh
saling relatif prima, diperoleh ![]() and
and ![]() adalah bilangan kuadrat. Artinya,
adalah bilangan kuadrat. Artinya, ![]() and
and ![]() untuk suatu bilagan bulat positif
untuk suatu bilagan bulat positif ![]() and
and ![]() . Karena
. Karena ![]() adalah bilangan ganjil,
adalah bilangan ganjil, ![]() dan
dan ![]() memiliki paritas yang berbeda. Akibatnya,
memiliki paritas yang berbeda. Akibatnya, ![]() dan
dan ![]() memiliki paritas yang berbeda.
memiliki paritas yang berbeda.
Sebaliknya, perhatikan bahwa
![]()
Artinya, ![]() atau
atau ![]() merupakan tripel Pythagoras. Lebih lanjut, tripel tersebut primitif sebab sebarang faktor persekutuan dari
merupakan tripel Pythagoras. Lebih lanjut, tripel tersebut primitif sebab sebarang faktor persekutuan dari ![]() dan
dan ![]() adalah bilangan ganjil dan merupakan faktor persekutuan dari
adalah bilangan ganjil dan merupakan faktor persekutuan dari ![]() dam
dam ![]() , sedangkan
, sedangkan ![]() .
.
[/learn_more]
Persamaan Pell
Persamaan Pell merupakan suatu persamaan Diophantine yang memiliki bentuk
(2) ![]()
dengan ![]() adalah suatu bilangan bulat positif.
adalah suatu bilangan bulat positif.
Dalam mencari solusi bulat persamaan Pell, cukup diselidiki solusi bulat positif dari persamaan tersebut.
- Jika
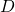 merupakan bilangan kuadrat, katakan
merupakan bilangan kuadrat, katakan 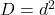 , maka solusi bulat persamaan Pell dapat dicari dengan menggunakan teknik pecah kuadrat:
, maka solusi bulat persamaan Pell dapat dicari dengan menggunakan teknik pecah kuadrat: 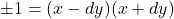 .
. - Jika
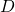 bukan bilangan kuadrat, terdapat tak hingga banyaknya solusi bulat persamaan Pell.
bukan bilangan kuadrat, terdapat tak hingga banyaknya solusi bulat persamaan Pell.
Teorema berikut memberikan solusi bulat positif persaman Pell ![]() .
.
Teorema 2
[box] Misalkan ![]() bukan bilangan kuadrat dan
bukan bilangan kuadrat dan ![]() merupakan solusi bulat positif terkecil (dengan
merupakan solusi bulat positif terkecil (dengan ![]() terkecil) dari persamaan
terkecil) dari persamaan ![]() . Semua solusi bulat positif persamaan Pell
. Semua solusi bulat positif persamaan Pell ![]() diberikan oleh pasangan bilangan bulat positif
diberikan oleh pasangan bilangan bulat positif ![]() ,
, ![]() , dengan
, dengan
![]()
[/box]
[learn_more caption=”Bukti:” state=”open”]
Perhatikan bahwa jika ![]() dan
dan ![]() adalah solusi bulat positif persamaan Pell tersebut, maka
adalah solusi bulat positif persamaan Pell tersebut, maka ![]() , yang berarti
, yang berarti ![]() merupakan solusi lain persamaan Pell. Berdasarkan observasi ini, solusi persamaan Pell
merupakan solusi lain persamaan Pell. Berdasarkan observasi ini, solusi persamaan Pell ![]() dapat diperoleh melalui ekspresi
dapat diperoleh melalui ekspresi ![]() , yakni
, yakni
![]()
atau ekuivalen dengan
![]()
Selanjutnya, akan ditunjukan tidak ada solusi lain selain bentuk di atas. Andaikan terdapat solusi bulat positif lain, katakan ![]() . Terdapat bilangan asli
. Terdapat bilangan asli ![]() dengan sifat
dengan sifat
![]()
Dengan mengalikan ketaksamaan tersebut dengan ![]() , diperoleh
, diperoleh
![]()
Akan tetapi,
![]()
yang berarti ![]() merupakan suatu solusi bulat positif yang lebih \textit{kecil} dari
merupakan suatu solusi bulat positif yang lebih \textit{kecil} dari ![]() , suatu kontradiksi.
, suatu kontradiksi.
[/learn_more]
Contoh :
Tentukan semua bilangan asli ![]() sehingga
sehingga ![]() merupakan bilangan kuadrat sempurna
merupakan bilangan kuadrat sempurna
Solusi :
Misalkan ![]() . Diperoleh
. Diperoleh
![]()
Cukup diselidiki solusi dari persamaan Pell: ![]() .
.
Dapat dicek bahwa ![]() merupakan solusi bulat positif terkecil. Dengan demikian, semua solusi berbentuk
merupakan solusi bulat positif terkecil. Dengan demikian, semua solusi berbentuk
![]()
atau ekuivalen dengan
![]()
Jadi, semua bilangan asli ![]() yang memenuhi berbentuk
yang memenuhi berbentuk ![]() dengan
dengan ![]() .
.
Teorema Terakhir Fermat
Teorema terakhir Fermat merupakan salah satu teorema yang terkenal dikalangan matematikawan yang bekerja di teori bilangan. Teorema ini terkait dengan eksistensi solusi bulat persamaan Diophantine berbentuk ![]() dengan
dengan ![]() bilangan asli. Mudah dicek bahwa untuk
bilangan asli. Mudah dicek bahwa untuk ![]() , persamaan tersebut memiliki tak hingga banyaknya solusi, sedangkan untuk
, persamaan tersebut memiliki tak hingga banyaknya solusi, sedangkan untuk ![]() , solusi bulat positif persamaan tersebut tiada lain adalah tripel Phytagoras. Untuk
, solusi bulat positif persamaan tersebut tiada lain adalah tripel Phytagoras. Untuk ![]() , eksistensi solusi persamaan tersebut diberikan dalam teorema berikut.
, eksistensi solusi persamaan tersebut diberikan dalam teorema berikut.
Teorema 3
[box] Diberikan ![]() . Persamaan Diophantine
. Persamaan Diophantine ![]() tidak memiliki solusi bulat.[/box]
tidak memiliki solusi bulat.[/box]
Pada awalnya, teorema ini masih berupa sebuah klaim. Klaim ini pertama kali disampaikan Fermat sekitar tahun 1637. Dalam tulisannya, ia juga menambahkan catatan bahwasanya ia memiliki solusi yang indah untuk klaim tersebut, namun tidak ada ruang yang cukup untuk menuliskannya. Setelah usaha yang keras selama 348 dari para matematikawan lainnya dalam membuktikan klaim tersebut, pada tahun 1994, Andrew Wiles berhasil membuktikan teorema tersebut untuk pertama kali dan ia mempublikasikannya pada tahun 1995. Bukti yang dituliskan oleh Andrew Wiles sendiri terdiri dari 200-an lebih halaman. Hal ini menunjukkan seberapa sulitnya untuk membuktikan teorema ini.
Selanjutnya, Pembaca dapat mengerjakan soal-soal berikut sebagai latihan.
- Tentukan bilangan bulat positif terbesar yang tidak dapat dinyatakan dalam bentuk
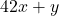 untuk suatu bilangan bulat positif
untuk suatu bilangan bulat positif 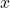 dan
dan 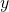 dengan
dengan 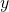 komposit.
komposit. - Tentukan semua bilangan asli
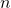 sehingga
sehingga 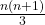 merupakan bilangan kuadrat sempurna.
merupakan bilangan kuadrat sempurna. - Tentukan semua solusi bulat positif persamaan
![Rendered by QuickLaTeX.com \[ x^2-4xy+y^2=1. \]](https://teoribilangan.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-6bb638f3a773d29f16777ef75b462139_l3.png)
0 Comments