Pada waktu sekolah dasar (SD), kita sudah dikenalkan dengan istilah kelipatan, faktor , FPK, dan KPK. Sebagai contoh, 24 merupakan kelipatan dari 6 dan 6 merupakan faktor dari 24. Dari contoh ini, kita bisa dengan mudah menentukan semua faktor dari 24, yakni 1,2,3,4,6,8,12, dan 24. Berdasarkan fakta ini, kita bisa dengan mudah menentukan semua bilangan positif ![]() yang merupakan faktor dari 24, yakni
yang merupakan faktor dari 24, yakni ![]() , dan
, dan ![]() . Bagaimana jika ditanyakan semua bilangan bulat positif
. Bagaimana jika ditanyakan semua bilangan bulat positif ![]() sehingga
sehingga ![]() merupakan faktor dari
merupakan faktor dari ![]() ? Untuk menjawab pertanyaan ini, pada artikel ini diberikan penjelasan mengenai keterbagian.
? Untuk menjawab pertanyaan ini, pada artikel ini diberikan penjelasan mengenai keterbagian.
Definisi 1.
[box] Diberikan bilangan bulat ![]() dan
dan ![]() dengan
dengan ![]() . Jika
. Jika ![]() merupakan kelipatan dari
merupakan kelipatan dari ![]() maka kita katakan
maka kita katakan ![]() habis membagi
habis membagi ![]() atau ditulis
atau ditulis ![]() . [/box]
. [/box]
Perlu dingat bahwa bilangan bulat ![]() merupakan kelipatan dari bilangan bulat
merupakan kelipatan dari bilangan bulat ![]() jika ada bilangan bulat
jika ada bilangan bulat ![]() sehingga
sehingga ![]() . Dengan demikian, Definisi 1 di atas ekuivalen dengan definisi berikut ini.
. Dengan demikian, Definisi 1 di atas ekuivalen dengan definisi berikut ini.
Definisi 2.
[box] Diberikan bilangan bulat ![]() dan
dan ![]() dengan
dengan ![]() . Bilangan
. Bilangan ![]() dikatakan habis membagi
dikatakan habis membagi ![]() jika terdapat bilangan bulat
jika terdapat bilangan bulat ![]() sedemikian sehingga
sedemikian sehingga ![]() .[/box]
.[/box]
Sebagai catatan, notasi ![]() dapat diartikan sebagai :
dapat diartikan sebagai :
 habis membagi
habis membagi 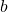
 adalah pembagi
adalah pembagi 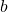 .
. adalah faktor dari
adalah faktor dari 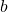
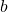 adalah kelipatan dari
adalah kelipatan dari  .
.
Dari definisi-definisi di atas, dapat diperoleh beberapa sifat berikut ini.
Teorema 1
Diberikan bilangan bulat ![]() ,
, ![]() dan
dan ![]() dengan
dengan ![]() . berlaku sifat-sifat dibawah ini :
. berlaku sifat-sifat dibawah ini :
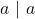 (setiap bilangan bulat
(setiap bilangan bulat 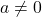 habis membagi dirinya sendiri)
habis membagi dirinya sendiri)- Jika
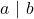 dan
dan 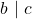 maka
maka 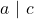 .
. - JIka
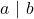 dan
dan 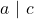 maka
maka 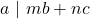 untuk setiap bilangan bulat
untuk setiap bilangan bulat 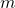 dan
dan 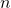 .
. - Jika
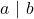 maka
maka 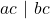
- Jika
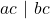 , maka
, maka 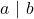 .
. 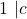 dan
dan 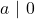 .
.- Jika
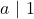 maka
maka 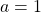 atau
atau 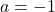 .
. - Jika
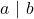 dan
dan 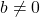 maka
maka 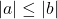
- Jika
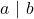 dan
dan 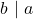 maka
maka 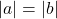
- Jika
 dan
dan 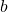 merupakan bilangan bulat positif, dan
merupakan bilangan bulat positif, dan 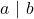 maka
maka 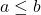
- Jika
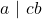 dan FBB
dan FBB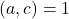 , maka
, maka 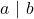
- Jika
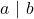 , dan
, dan 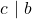 serta
serta 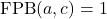 , maka
, maka 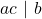
Untuk memahami penggunaan Teorema 1 di atas, diperhatikan contoh-contoh berikut ini
Contoh 1
Tentukan semua bilangan asli ![]() sehingga
sehingga ![]() .
.
Solusi: bilangan asli ![]() yang memenuhi
yang memenuhi ![]() adalah
adalah ![]() .
.
Contoh 2
Tentukan semua bilangan asli ![]() sehingga
sehingga ![]() merupakan bilangan bulat.
merupakan bilangan bulat.
Solusi : agar ![]() merupakan bilangan bulat, maka haruslah
merupakan bilangan bulat, maka haruslah ![]()
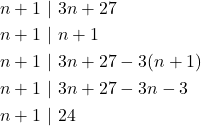
Karena ![]() merupakan bilangan asli, maka
merupakan bilangan asli, maka ![]() , sehingga diperoleh
, sehingga diperoleh ![]() . Dengan kata lain, nilai bilangan asli
. Dengan kata lain, nilai bilangan asli ![]() yang memenuhi adalah
yang memenuhi adalah ![]() .
.
Contoh 3:
Tentukan bulat positif ![]() sehingga
sehingga ![]() merupakan faktor dari
merupakan faktor dari ![]()
Solusi : Diiketahui bahwa ![]()
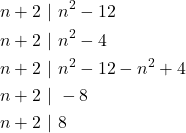
Karena ![]() merupakan bilangan asli, maka
merupakan bilangan asli, maka ![]() , sehingga diperoleh
, sehingga diperoleh ![]() . Dengan kata lain, nilai bilangan asli
. Dengan kata lain, nilai bilangan asli ![]() yang memenuhi adalah
yang memenuhi adalah ![]() dan
dan ![]() ..
..
0 Comments