Di dalam toples Andi, terdapat ![]() permen. Andi mengambil
permen. Andi mengambil ![]() permen untuk dia berikan kepada
permen untuk dia berikan kepada ![]() temannya dimana masing-masing mendapatkan
temannya dimana masing-masing mendapatkan ![]() permen, sehingga permen Andi tersisa
permen, sehingga permen Andi tersisa ![]() buah. Lalu Andi mengambil
buah. Lalu Andi mengambil ![]() permen lagi untuk dibagikan kepada
permen lagi untuk dibagikan kepada ![]() teman tadi dengan cara yang sama, berakibat permen di toples tersisa
teman tadi dengan cara yang sama, berakibat permen di toples tersisa ![]() buah. Proses tersebut Andi lakukan secara terus-menerus sampai permen di toples kurang dari
buah. Proses tersebut Andi lakukan secara terus-menerus sampai permen di toples kurang dari ![]() .
.
Kita dapat menghitung bahwa Andi melakukan proses tersebut ![]() kali, sehingga masing-masing teman Andi mendapatkan
kali, sehingga masing-masing teman Andi mendapatkan ![]() buah permen. Di sisi lain, kita juga dengan mudah mengetahui bahwa sisa permen di dalam toples Andi adalah
buah permen. Di sisi lain, kita juga dengan mudah mengetahui bahwa sisa permen di dalam toples Andi adalah ![]() buah permen.
buah permen.
Secara matematis, ini dapat kita tuliskan sebagai ![]() atau
atau ![]() , dimana 19 kita katakan sebagai hasil bagi dan
, dimana 19 kita katakan sebagai hasil bagi dan ![]() adalah sisa pembagian.
adalah sisa pembagian.
Permasalahan di atas dapat digeneralisasi menjadi sebuah teorema yang terlihat cukup trivial, namun sangat berguna.
Teorema [Algoritma Pembagian] [box]
Untuk setiap bilangan bulat positif ![]() dan
dan ![]() terdapat dengan tunggal pasangan bilangan bulat non-negatif
terdapat dengan tunggal pasangan bilangan bulat non-negatif ![]() sedemikian sehingga
sedemikian sehingga ![]() dimana
dimana ![]() . Selanjutnya,
. Selanjutnya, ![]() dikatakan sebagai \textbf{hasil bagi} dan
dikatakan sebagai \textbf{hasil bagi} dan ![]() adalah \textbf{sisa pembagian} ketika
adalah \textbf{sisa pembagian} ketika ![]() dibagi oleh
dibagi oleh ![]() .[/box]
.[/box]
[learn_more caption=”Bukti:” state=”open”] Pertama, ditunjukkan eksistensi ![]() . Dibagi 3 kasus.
. Dibagi 3 kasus.
Kasus 1: ![]() .
.
Jika ![]() , dapat dipilih
, dapat dipilih ![]() dan
dan ![]() , sehingga dapat dituliskan dalam
, sehingga dapat dituliskan dalam
![]()
Dalam kasus ini, kita peroleh pasangan ![]() .
.
Kasus 2: ![]() .
.
Jika ![]() , dapat dipilih
, dapat dipilih ![]() dan
dan ![]() sehingga dapat dituliskan dalam
sehingga dapat dituliskan dalam
![]()
Untuk kasus ini, diperoleh pasangan ![]() .
.
Kasus 3: ![]() .
.
Diasumsikan ![]() . Terdapat bilangan asli
. Terdapat bilangan asli ![]() sehingga
sehingga ![]() . Karena himpunan bilangan asli \textit{well-ordered}, terdapat bilangan asli terkecil
. Karena himpunan bilangan asli \textit{well-ordered}, terdapat bilangan asli terkecil ![]() sehingga
sehingga ![]() . Berdasarkan minimalitas
. Berdasarkan minimalitas ![]() , kita peroleh
, kita peroleh ![]() .
.
Dengan memilih ![]() , didapat
, didapat ![]() dengan
dengan ![]() .
.
Dari 3 kasus di atas, kita telah membuktikan eksistensi ![]() . Selanjutnya, akan dibuktikan ketunggalannya.
. Selanjutnya, akan dibuktikan ketunggalannya.
Diasumsikan terdapat ![]() yang juga memenuhi
yang juga memenuhi ![]() dengan
dengan ![]() . Oleh karena itu, kita peroleh
. Oleh karena itu, kita peroleh
![]()
Sehingga ![]() . Dengan sifat keterbagian, maka
. Dengan sifat keterbagian, maka ![]() atau
atau ![]() . Karena
. Karena ![]() , maka
, maka ![]() dan menyebabkan
dan menyebabkan ![]() tidak mungkin. Ini berakibat
tidak mungkin. Ini berakibat ![]() , yang terpenuhi hanya saat
, yang terpenuhi hanya saat ![]() . Dengan mudah kita juga akan memperoleh
. Dengan mudah kita juga akan memperoleh ![]() . Ketunggalan terbukti. [/learn_more]
. Ketunggalan terbukti. [/learn_more]
Teorema di atas menjamin setiap pembagian dua bilangan asli akan menghasilkan hasil bagi dan sisa yang unik (tunggal).
Teorema di atas dapat diperluas menjadi bilangan bulat.
Teorema [Generalisasi Algoritma Pembagian]
[box] Untuk sebarangn bilangan bulat ![]() dan
dan ![]() dimana
dimana ![]() , terdapat dengan tunggal pasangan bilangan bulat
, terdapat dengan tunggal pasangan bilangan bulat ![]() sedemikian sehingga
sedemikian sehingga ![]() dan
dan ![]() .
.
[/box]
Berikut adalah contoh penggunaan algoritma pembagian.
- Bilangan genap
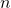 dapat dinyatakan dalam
dapat dinyatakan dalam 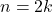 dimana
dimana 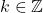 .
. - Bilangan ganjil
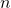 dapat dinyatakan dalam
dapat dinyatakan dalam 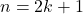 dimana
dimana 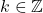 .
. - Untuk setiap bilangan bulat
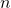 ,
, 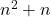 adalah bilangan genap.
adalah bilangan genap. - Jika
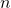 bilangan bulat yang tidak habis dibagi 3, maka
bilangan bulat yang tidak habis dibagi 3, maka 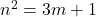 untuk suatu bilangan bulat
untuk suatu bilangan bulat 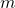 .
. - Jika
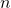 bilangan ganjil, maka
bilangan ganjil, maka 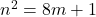 untuk suatu bilangan bulat
untuk suatu bilangan bulat 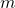 .
. - Jika
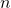 bilangan bulat,
bilangan bulat, 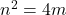 atau
atau 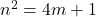 untuk suatu bilangan bulat (non-negatif)
untuk suatu bilangan bulat (non-negatif) 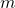 .
. - Jika
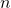 bilangan genap,
bilangan genap, 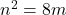 atau
atau 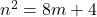 untuk suatu bilangan bulat (non-negatif)
untuk suatu bilangan bulat (non-negatif) 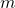 .
. - Jika
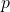 adalah bilangan prima yang lebih besar dari 3, maka
adalah bilangan prima yang lebih besar dari 3, maka 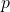 dapat dinyatakan dalam
dapat dinyatakan dalam 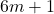 atau
atau 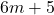 untuk suatu bilangan bulat
untuk suatu bilangan bulat 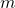 .
.
Bukti contoh penggunaan contoh di atas dapat digunakan Pembaca sebagai latihan.
0 Comments